Multiple External Representations in Dynamic Geometry: a Domain-Informed Design

Abstract

Designing an effective Multiple External Representations (MERs) environment remains a difficult task, as research that has evaluated how they support learning has produced mixed results. Different approaches can be used to complete this effectiveness objective. One such approach, defined as Domain-Informed, may consist in starting with and fitting in pedagogical analysis of the domain, which required the active collaboration of experts in the design process itself. Such a participatory design was initiated for the conception of Calques 3D, a three-dimensional dynamic geometry microworld. This paper describes the external representations available in the software, their pedagogical purpose and the decisions and problems that have occurred during the participatory design process.

INTRODUCTION

Multiple External Representations (MERs) is widely used in Learning Environments, in the hope that learners can benefit from the properties of each representation and ultimately achieve a deeper understanding of the subject being taught. But designing an effective multirepresentational environment remains a difficult task, as research that has evaluated how they support learning has produced mixed results. Different approaches can be used to complete this effectiveness objective. One such approach, which can be defined as Domain-Informed, consists in starting with and fitting in pedagogical analysis of the domain, which required the active collaboration of experts in the design process itself. Such a participatory design was initiated for the conception of Calques 3D [], a dynamic geometry microworld.

Our goal was to develop materials and techniques that would allow us, without the assistance of knowledge engineers, to extract the implicit knowledge that teachers have about "how and why they teach concepts in particular ways". We needed to find ways in which we could help them make explicit not only what steps they used in building their lessons (extracting concepts) but also how they wanted to present their ideas (extracting pedagogy). The key element in our work has been the design of several forms that teachers are requested to use in the description of how they present the topics they will cover []. During all the stages of the design cycles, a group of mathematics teachers was closely integrated in the definition of the pedagogical content of the environment, in the specification and evaluation of the HCI, especially on the refinement of the external representations of the domain’s concepts.

In this paper, I will describe the design of the External Representations in Calques 3D, focusing especially on the design decisions and problems that occurred during this participatory process. I will conclude the paper and open the discussion by highlighting how other approaches can be used for designing effective MER Learning Environment.

CALQUES 3D, A 3D DYNAMIC GEOMETRY MICROWORLD

Calques 3D is a Dynamic Geometry microworld [, ] designed for constructing, observing and manipulating geometrical figures in space. It allows an intuitive and adaptable access to environment features. Intuitive because it is used by students who do not have preparation. Adaptable because it allows the teacher to decide, with respect to his own pedagogy, which primitives and operations will be made available to the students. The aims of Calques 3D are threefold:

• Observation: allowing one to see and understand the third dimension by changing the spatial system of reference (axes, floor, etc.), choosing perspective ('cavalière', vanishing point, etc.), modifying the observer's point of view; displaying visual feedback on objects, etc.
• Construction: allowing a dynamic construction of geometrical figures from elementary objects (points, lines, planes, etc.) and construction primitives (intersection, parallel, perpendicular, etc.).
• Exploration: allowing one to explore and discover geometrical properties of the figure (deforming it by directly dragging base-points, changing observer's point of view, etc.).

The following text is an example of an assignment that could be deliverer to learners:

Let ABCDE be a regular square-base pyramid.
Let I be a point that belongs to the height of the pyramid.
Let Pl be a plane perpendicular to the height of the pyramid and going through I.
What is the nature of the section of the pyramid ABCDE by the plane Pl?

The learners may start the construction from scratch or use a predefined figure, depending on the nature and difficulty of the activity settled by the teacher.

CALQUES 3D, A MER LEARNING ENVIRONMENT

Following the teachers’ requirements expressed during the participatory design and according to the pedagogical objectives of Calques 3D, several External Representations were defined (see Figure 1), each of them with a particular pedagogical role:

1. Universe: a graphical ER that represents the drawing of the geometrical figure;
2. Tracings: a particular instance of the Universe ER where only parts of the figure are displayed;
3. History: a textual ER, which represents the declarative description of the figure. Two other ERs were added more recently, on a pure theoretical basis, in order to expand the domain’s coverage and to try to improve the learners’ understanding of the dynamic geometry paradigm:
4. MathPad: an algebraic ER that allows the learners to access to the algebraic form of some selected objects of the figure (i.e. equation of planes, coordinates of points, measure of volumes, distances and angles, etc.);
5. Graph: a diagrammatic ER that represents the structural dependency graph of the figure.

Figure 1

A Snapshot of the Calques 3D interface with the different ERs (from top to bottom and from left to right): the Universe, the History, a Tracing, the MathPad and the Graph.

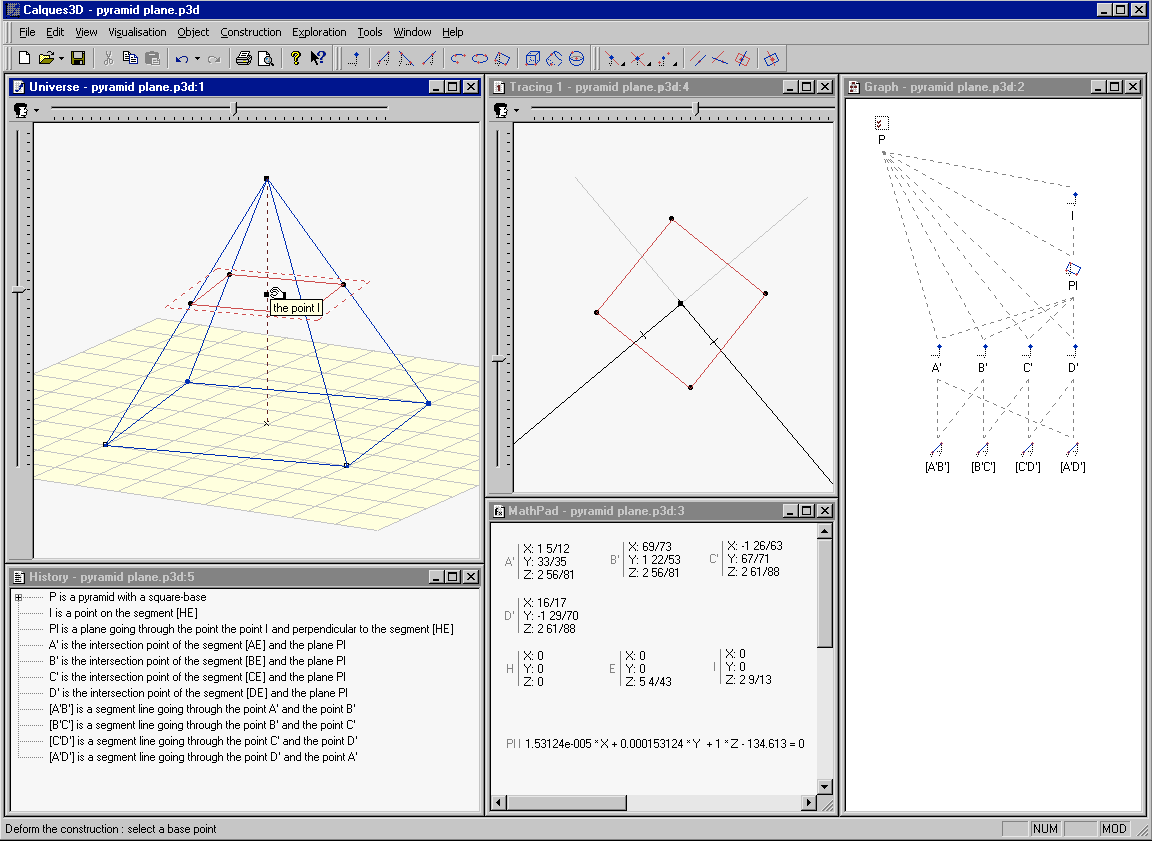
Figure 1

A Snapshot of the Calques 3D interface with the different ERs (from top to bottom and from left to right): the Universe, the History, a Tracing, the MathPad and the Graph.

All these external representations were designed independently, but they all contribute to a common purpose in the learning process: to support knowledge transfer by learners. As a microworld, i.e. designed with a strong constructivist approach, the emphasis was placed on the feedbacks provided to learners, in particular as a support for mapping entities across ERs. Consequently, External Representations in Calques 3D are fully dyna-linked: the selection of an object in one ER results in highlighting it in the others; any deformation of the construction results in the immediate update of the tracings, MathPad and other ERs; etc.

The Universe External Representation

In accord with the pedagogical objective of Calques 3D, the Universe is the central and privileged ER of the microworld: it is the place where most of the operations realised by the learners in order to construct, observe and manipulate the geometrical figure will occur.

Not surprisingly, the conception of this ER has required most of the design decisions, in order to provide the learners with sufficient supports for helping them to visualise geometrical objects and moving from a concrete to an abstract environment. The use of a direct manipulation interface [, ] for constructing the figure or deforming it in order to explore different configurations was such a decision. But the definition of the format of this ER required a careful consideration, as it was important to bridge the gap between the geometrical concept and its 2D or 3D representations, i.e. grasp the difference between figure and drawing []. So the expertise of the teachers involved in the design process, as with some trial-and-errors, allowed us to determine how to materialise the space (introducing some visual system of reference like the axes, the floor, etc.), how to represent the geometrical objects (in particular the infinite ones like the plane or the volumes like the sphere), how to symbolise the geometrical relations involved in the figure (supporting the learners in reading the figure), etc.

The Tracing External Representations

The tracing External Representation is a particular instance of the Universe ER, in the sense that both have the same formats and operators, but the tracing does not allow the learners to construct or add objects to the figure: only the observation and manipulation primitives are available. The intended purpose of this ER was to provide the learners with a way to perform a visual filtering of the main construction represented in the Universe ER, i.e. to allow them to extract and observe parts of the construction in an independent view. The main pedagogical purpose of this ER is to allow the learners to focus on a reduced part of the whole construction (i.e. free of ‘noise’) in order to take hold of it and, then, reapply this knowledge to the whole figure.

Figure 2

The Universe External Representation (left) displays the whole construction of the problem; the tracing ER (right) only displays the section of the pyramid, with a different projection (different observer’s point of view and spatial system of reference).

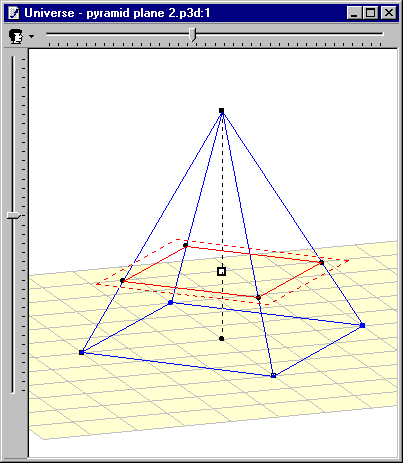
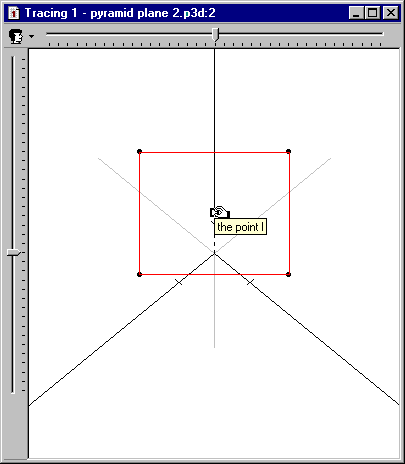
Figure 2

The Universe External Representation (left) displays the whole construction of the problem; the tracing ER (right) only displays the section of the pyramid, with a different projection (different observer’s point of view and spatial system of reference).

The design of this ER raised a very interesting problem that could be related to possible discrepancies between theoretical approach and pedagogical practice. In theory, both the universe and the different tracings should have different and independent formats, as they represent different external representations of the domain’s concepts. In practice, it means that a figure could be visualised simultaneously with different projections (i.e. different observer’s points of view, different spatial systems of reference) and with different shapes (i.e. different colours and/or different line sizes for a single object). After experimentation, the teachers considered the former as a desired and useful feature. However, they rejected the latter as a very annoying and misleading feature. The reason of such a rejection lies in the fact that different shapes across ERs for a single object may not allow the learner to effectively map the entities, i.e. to quickly identify the different representations as different instances of the same object. It was argued that different projections may also introduce such a gap, but the potential outcomes of this feature certainly balance its limitations.

The History External Representation

The main function of the History ER (Figure 3) is to provide the learners with a textual and chronological list of all the geometrical objects involved in the construction of the figure. In a way, it can be viewed as the text of the figure, i.e. a procedural description of its construction: the nature of the objects and the relations used to construct the figure are explicitly stated but no information about their spatial location is displayed. This function was a strong teachers’ requirement for the design, especially because of its familiarity with the text in paper-and-pencil approach. But its subsequent experimentations during the design and evaluation process led us to improve its usability by adding two new major usages: an explanatory purpose and a shortcut to the objects’ attributes.

Calques 3D being a microworld, providing the learners with the explanations related to the Euclidean Geometry remain under the teachers’ responsibility but the software has to handle those related to the Dynamic Geometry, in particular those introduced by the dynamic feature and the manipulation of different configurations of a geometrical figure. For example, a point at the intersection of two segment lines may or may not be defined, depending on the configuration of the two segments, but even if undefined, it is still part of the figure, as explicitly constructed by the learners. In such a situation, the corresponding items in the History are displayed with a particular format (e.g. in red or with a dedicated icon in front of the text) to represent its undefined status. Moreover, one can double-click on the item in order to obtain a precise explanation about the reasons of this status (with sentences like “the point is not defined because the segments do not intersect”).

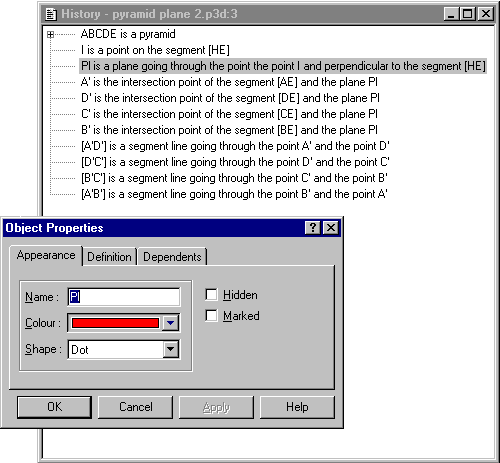
Figure 3

Selecting an item in the History External Representation (left) will highlight it in the Universe ER (right); double-clicking on it will allow the learner to access on its properties.

Figure 3

Selecting an item in the History External Representation (left) will highlight it in the Universe ER (right); double-clicking on it will allow the learner to access on its properties.

The direct manipulation of the figure was a constant concern during the design, both for usability and learning, as this ‘real-world’ metaphor improves the continuity between domain and its external representations. But this paradigm may be subjected to strong weaknesses in some situation, e.g. when the learners try to gain access to a single precise object in order to change some of its attributes (i.e. colour, name, visibility, etc.). In a complex construction, such an action may be difficult to operate because of the ‘noise’ created by all the irrelevant displayed part of figure, a situation which is worse (i.e. more ambiguous) in three dimensions than in two dimensions. Thus, because of its format, the History provides the learners with a very convenient way of accessing individual objects in the construction.

The MathPad External Representation

There are two motivations for handling the analytical information of a figure as an external representation. First, the main pedagogical objective of Calques 3D is the observation of the visual representation of geometrical objects; consequently accessing the analytical component of geometry is and will remain an alternative motive, related to other pedagogical situations. Second, the paper-and-pencil metaphor, widely used in the two-dimensional dynamic geometry software like Cabri [] or Geometer’s Sketchpad [], in which different reifications of the domain’s concepts (i.e. visual objects, equations, explanation texts, etc.) are mixed up in the same external representation, does not successfully fit anymore in a three-dimensional environment. Building an external representation for the sole purpose of the analytical register can solve both of these problems: it can be accessing only on the appropriate pedagogical situation and its format can be defined in accordance to the paper-and-pencil metaphor.

The MathPad external representation (Figure 4) allows the learners to access to an algebraic representation of requested objects – like the coordinates of a point or the equation of a plane, etc. – or geometrical properties – like the distance between two points, the angle between two lines, etc. In its current state of development, this ER is only for a display purpose but it will improve in the future, providing the learners with more interaction (e.g. changing the location of a point by editing its coordinates).

Figure 4

The MathPad external representation, displaying the coordinates of some selected points (1), the equation of a plane (2) and a couple of distance between points (3).

Figure 4

The MathPad external representation, displaying the coordinates of some selected points (1), the equation of a plane (2) and a couple of distance between points (3).

The Graph External Representation

As mentioned above, there is a major difference between dynamic geometry and Euclidean geometry, which lies in the dynamic aspect of the domain’s implementation. The History ER can play an important role in providing the learners with explanations about the behaviour of the construction when exploring its different configurations, but we thought that it might be not sufficient and that an explicit representation of the internal structure of the construction may improve its understanding by learners.

When constructing a geometrical figure, the learners have to formally describe how elementary geometrical objects (e.g. points, lines, planes, etc.) are related altogether with a particular geometrical relation (e.g. parallel, perpendicular, belong to, etc.). This step-by-step construction results in establishing a dependency graph (see figure 5) of the construction, where nodes represent the elementary objects and arcs represent the geometrical relations that links them. During a deformation of the construction, when the learner moves it to another configuration, some prerequisite properties may not be verified for an object to be defined (such as the intersection of two segments), resulting in the disabling of a whole part of the graph (propagation in the child nodes). An external representation of this structural graph, which will display such undefined parts of the construction, may be able to stress an unclear behaviour of the construction. The format of this ER should be carefully designed, as a construction will imply a complex and useless graph. For examples Graph pruning and reduction procedures could be used in order to focus on interesting parts, either at learner’s or system’s initiative.

Figure 5

The Graph ER provides the learners with an access to the internal structure of the geometrical construction, by displaying the parents (1) or the children (2) of the selected object.

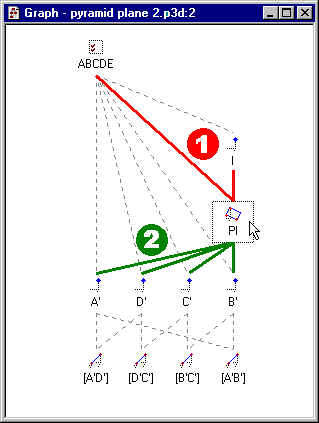
Figure 5

The Graph ER provides the learners with an access to the internal structure of the geometrical construction, by displaying the parents (1) or the children (2) of the selected object.

Actually, there is no evidence, neither theoretical nor empirical, for such an external representation to be useful in the learning process; as far as we know, the explicit use of the structural graph in coordination with the ‘traditional’ graphical and textual ERs in geometry was never studied. Further experimentations would allow us to clarify this proposal.

DISCUSSION

The participatory design process used for the conception of Calques 3D was an example of a Domain-Informed Design approach, which led to the definition and the design of effective external representations, according to the requirements and needs of teachers involved in the process. But this is not the sole approach, neither we claim it covers every aspects of educational software engineering. In particular, the external representations in Calques 3D were not treated as a whole topic, but rather individually and independently. Roughly speaking, it means that Calques 3D could be view more as a Several External Representation Learning Environment rather than a Multiple External Representation Learning Environment. A more unified, Representational- Informed Design approach, should be processed, starting from cognitive issues, rather than with pedagogical issues. Such an approach could be supported with an appropriate conceptual framework, such as DeFT [, ]. The DeFT (Design, Functions, Tasks) framework for multi-representational learning environments sets out a number of important questions that designers and teachers should ask in order to provide effective learning experiences for their students. It provides an account of the different pedagogical functions that multiple representations can play (such has having a complementary role, constraining the interpretation or constructing a deeper understanding), the design parameters that are unique to learning with more than one representation (such as informational redundancy, sequencing and ordering, translation support) and the cognitive tasks that must be undertaken by a learner when interacting with MERs. (such as the understanding of the properties of the representation, the relation between an ER and the domain).

It is not our claim that Domain-Informed Design and Representational-Informed Design are antagonist approaches but, on the contrary, that they provide one with potential concurrent and complementary analysis for a better and effective design of multi-representational learning environments. Using the DeFT framework for running a retrospective analysis of Calques 3D, as we propose to do in the next stages of our research agenda, can lead us to refine the pedagogical requirements integrated in the external representations design. The question we have to keep in mind is: Where does Calques 3D fit in the design space defined by this framework – in term of design parameters, in term of functions and in term of tasks?

REFERENCES