IF "What is the Core of AI & Education?" Is the Question THEN "Teaching Knowledge" is the Answer

Abstract

This paper emphasizes the importance of capturing, i.e. making explicit, the knowledge that teachers implicitly use in teaching - the content as well as pedagogy. We describe a process for obtaining information from geometry teachers that will help us to better understand how they teach the spatial properties inherent in 3D geometry. This in turn enables us to improve the design of special software we have built (Calques 3D) based on their requests to have software that will help them bridge the gap between their current ways of teaching and the objective of having their students better prepared for the world of Computer Assisted Design. We describe the tools (forms) we use to capture this information and the results we experience - both the advantages and problems.

1. Introduction

Acquiring knowledge from people (usually experts) is well-known as a difficult problem (see and ). In order to extract this knowledge one often utilizes the assistance of a knowledge engineer (For example, see for a cogent overview of this process). However, a knowledge engineer is often not available or too expensive, especially when one is working in education. Our goal was to develop materials and techniques that would allow us, without the assistance of knowledge engineers, to extract the implicit knowledge that teachers have about "how and why they teach concepts in particular ways". This was important because we were trying to assist Geometry teachers to most effectively and seamlessly integrate a software tool, Calques 3D, that had been developed in our lab into their way of teaching spatial properties of geometry. Thus, we needed to find ways in which we could help them make explicit not only what steps they used in building their lessons (extracting concepts) but also how they wanted to present their ideas (extracting pedagogy).

This paper describes how we attempted to solve this problem, the results we have achieved, and the problems we experienced. The key element in our work has been the design of several forms that teachers are requested to use in the description of how they present the topics they will cover. Previous work done by several of the authors (, and ) as well as others (see for example) has shown the importance of integrating the teachers in the design process of developing and using educational software. In our experience it is necessary to extend this participation from not only assisting in the design of the software but to the way it will actually be used in the classroom. In order to do that effectively we needed to better understand how the teachers taught different concepts so they could help us prepare links between how they taught and how they could use Calques 3D to help them achieve their teaching objectives.

We begin with a brief description of the Interactive Learning Environment we have built to assist geometry teachers in their visual presentation of spatial geometry concepts. A discussion of the rationale and design of the forms follows this overview . The remaining sections of the paper discuss our experiences with the teachers using the forms, an assessment of their usefulness and ideas we have for extending this work. The cornerstone for our work is that Teaching Knowledge, though elusive, needs to be well understood if we are to achieve maximum success with the use of educational software. The utilization of forms such as those discussed in this paper is one way to help extract this information.

2. An Interactive Learning Environment for spatial geometry

Calques 3D is a microworld, i.e. a type of Interactive Learning Environment (ILE), designed for constructing, observing and manipulating geometrical figures. It provides students an intuitive and adaptable access to environment features. Intuitive because it is used by students who do not have preparation and adaptable because it allows teachers to decide, with respect to their own pedagogy, which primitives and operations will be made available to students. The aims of Calques 3D are threefold :

• observation : allowing one to see and understand the third dimension by changing the spatial system of reference (e.g. axes, floor, etc.), choosing perspective (e.g. cavalier, vanishing point, etc.), modifying the observer's point of view (e.g. a frontal point of view for 'real-sized' observation), displaying visual feedback on objects (e.g. projection of points' co-ordinates on the horizontal plane), etc.
• construction : allowing a student to dynamically construct geometrical figures from elementary objects (points, lines, planes, etc.) and construction primitives (intersection, parallel, perpendicular, etc.).
• exploration : allowing one to explore and discover geometrical properties of the figure (deforming it by directly dragging base-points, extracting geometrical objects in separate synchronized tracings, etc.).

As a dynamic geometry environment, our project is built on similar research, both in plane geometry, e.g. Geometer's Sketchpad , Cabri-geometry , Calques 2 , and in spatial geometry, e.g. Cabri 3D .

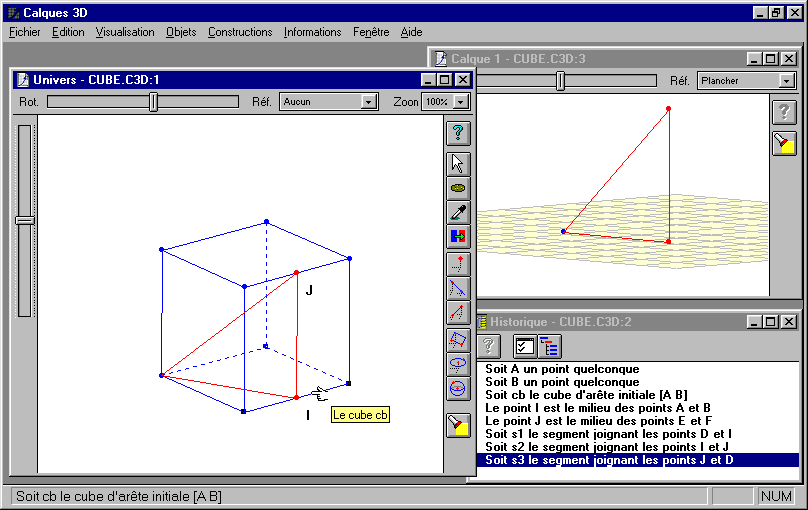
The plane representation of a spatial figure (i.e. the drawing of the figure) does not provide enough visual information to allow students to understand all its geometrical properties, even if they could modify the observer's point of view. However, the dynamic deformation of such a figure does provide the user with another way of exploring it. This exploration of figures is realized through an interface based on an extension of the direct manipulation concept for spatial environments. During the point dragging, Calques 3D maintains the coherence of the relations either explicitly specified in the figure or resulting from the construction, and calculates and redraws in real-time the new shape of the construction. Figure 1 shows an example as the student would see it on the screen.

Figure 1

Geometrical relations between the cube and the triangle (extracted from one of its sides) are maintained during any deformation of the cube.

Figure 1

Geometrical relations between the cube and the triangle (extracted from one of its sides) are maintained during any deformation of the cube.

3. A framework for extracting implicit teacher knowledge

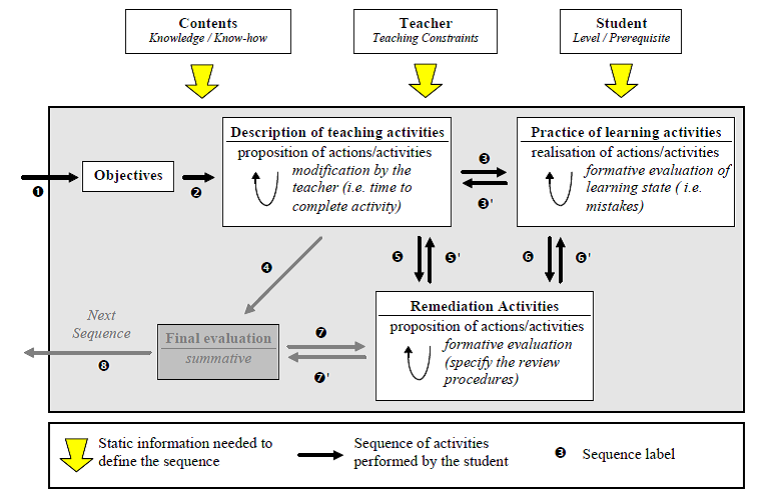
Figure 3 provides an overview of a pedagogical sequence that describes different components of teaching activities . This model proposes that teachers view their presentation from three perspectives: contents (domain knowledge), student learning goals (as seen by the teachers) and their own teaching process to achieve these goals. The most important part of this model for us are the boxes representing the activities "Description of teaching", "Practice of learning" and "Remediation". We have tried to capture this information, which we call "Teaching Knowledge", by asking teachers to fill out forms which break these general activities into finer grained pieces. For example, we replace the less precise idea of "Description of teaching activities" with the more specific request for information on "Objectives of the Sequence" and "Activities of the Sequence".

Figure 3 and Figure 4 are the specific forms we used to extract detailed information about "teaching knowledge" - both HOW teachers present the information and WHY they have chosen this method. In the work we report here we have collaborated with a group of teachers who teach dynamic geometry as part of a course they give in technical schools to students in a general curriculum as well as to students in a "technicians" curriculum (i.e. technical draftsman, TV repairman, etc.). Each of them has been teaching this material for more than 20 years and it is their wisdom and expertise that we are trying to capture.

Figure 2

Overview of a pedagogical sequence.

Figure 2

Overview of a pedagogical sequence.

Our goal was to design these forms based on the model shown in Figure 2 in order to extract the teaching knowledge that teachers implicitly use. We realized that the forms had to be close enough to the teachers' way of thinking and describing pedagogical sequences BUT also needed to provide the type of information that we could incorporate in order to improve Calques 3D and its application in the classroom. That is why the forms are based on description of activities rather than on description of the general pedagogical sequence. Moreover, according to the objectives of Calques 3D, we focus on activities that involve visualization, construction and manipulation skills. Thus, at this stage of the project, we do not try to obtain data on every part of the pedagogical sequence (e.g. with final summative evaluation). We only ask the teachers to describe the most relevant activities (i.e. activities related to information and operation sequence objectives, see section D of Figure 3).

Figure 3

Figure 3: Description of a pedagogical sequence (annotations are in italics).

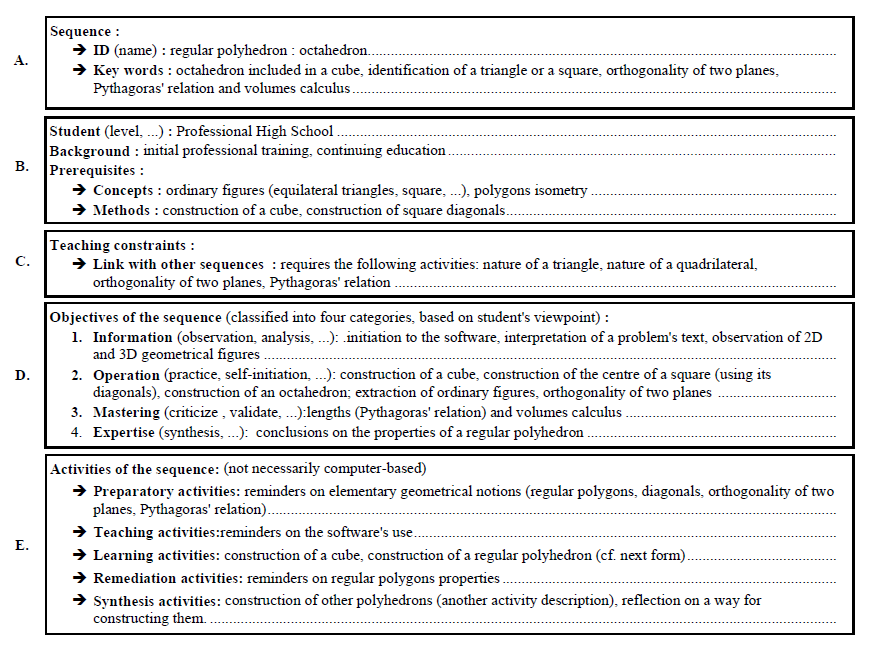
Figure 3

Figure 3: Description of a pedagogical sequence (annotations are in italics).

Figure 3 provides an annotated version of how we obtain information from the teachers with respect to the sequence of steps they use to help students understand the concepts they are trying to convey (in this case in dynamic geometry). It is important to note two aspects of this form: 1) It is designed to assist us to understand the way they teach, NOT necessarily to help them to improve their teaching by making their steps more explicit (even though they can draw benefits from describing those steps carefully) and 2) the form describes the general attributes most teachers take into account in developing a lesson, i.e. the form is NOT designed specifically to be used with geometry teachers. Many aspects of the form are self-explanatory. However, it is important to draw the readers attention to the following points.

1. Section D, the "Objectives of the sequence", is presented from the viewpoint of the student. As we will discuss later this has been one of the most difficult aspects for teachers to explicitly describe. While they are able to provide these descriptions in general, it is difficult for them to illustrate these items with concrete examples without first observing students using this specific software.
2. In section E, "Activities of the sequence", we found that the teachers concentrated almost exclusively on the computer-based activities they wanted to incorporate into their lessons. However, our objective here was to have them explicate their overall approach - the lecture/non-computer based activities (demonstrations with physical objects, drawings on the blackboard, etc.) as well as the use of Calques 3D for various purposes. This will also be discussed in more detail in section 4.

Figure 4 is the annotated description of the computer-based activities that they propose to incorporate into their lessons. It is the last two sections of this form that provide particularly useful information. For example, in Section B if the teachers can identify factual mistakes that students often make then we can concentrate on providing support using Calques 3D to help students overcome these mistakes (preemptive mode).

Figure 4

Description of computer-based activities in the sequence (annotations are in italics).

Figure 4

Description of computer-based activities in the sequence (annotations are in italics).

Moreover, once the teachers have explicitly catalogued certain student mistakes then we can work with them to evaluate how best to rectify the errors when they are made (remediation mode). A key decision is to ascertain whether it is better to provide a computer-based solution or another alternative .

Section C in Figure 4 is perhaps the most informative. This table summarizes some of the causal errors that teachers have identified and ways that we can address them. For example, if the student does not understand a term, then using a dictionary (off-line or computer-based) is a good solution. Or if the student is lacking some "know-how", for example, how to construct a parallelogram, then a demonstration might be most useful. Note that we have used the term "know-how" to indicate knowledge of the system as opposed to knowledge as applied to concepts. So continuing with this example, if the student does not know what a parallelogram is then we would provide a definition and example.

We experienced a problem in having the teachers provide information in this section. Instead of describing a set of problems they had encountered in teaching this material they thought we wanted them to identify errors students made in using Calques 3D. Given their unfamiliarity in using this software it was difficult for them to imagine what problems students might encounter. Once we explained that the form had a more global purpose, the gathering of typical student mistakes in learning dynamic geometry, they were able to provide us with the information we were seeking. This discussion also was important as part of the teachers comprehending the "larger picture" which was our effort to better understand their overall teaching process (knowledge) so that we could improve the design of the software and accompanying documentation for the use of a broad class of teachers. Based on this experience we realized that we need teachers for their teaching knowledge, but they need some preliminary training in order to become effective and efficient partners in this software design task, and that step was missing here. Even if there were more support for these teachers (i.e. some release time from teaching) this task remains quite difficult because of their lack of experience in teaching in a computer-based environment. We are confounding the teacher's existing expertise by asking them to invent a computer-based one, including fundamental changes in the relative importance and difficulty of teaching each concept or know-how.

4. Evaluation of using these forms

The teachers have been very conscientious about using the forms and providing us feedback. As noted in the previous section we soon found that there were some difficulties - understandable on the one hand but difficult to predict on the other! Following are some of the observations we made about the problems we encountered in using this method to extract "Teaching Knowledge" ; both with respect to the design of these forms as well as the use of such forms for more general knowledge acquisition.

Among the advantages of using forms like these are:

1. Provides us (and the teachers) with a better understanding of why they present geometry concepts as a series of connected activities; this seems especially important as they investigate ways to seamlessly integrate a new piece of software (Calques 3D) into their current way of presenting material or, alternatively, deciding whether this software actually allows them to teach in a different and better way.

2. A major reason that teachers are interested in using educational software is to motivate students. They realize this intuitively. But the key is to get them to translate this intuition into concrete uses of the software. In our case this problem was greatly simplified by having the teachers explicitly record the steps in their teaching process and provide us (and them) with a clear picture of how Calques 3D could be used to convey key dynamic geometrical properties that could not be effectively presented otherwise, e.g. for a correct visualization of the poles of a sphere , which students often misplace on its apparent contour when asked to draw them (see Figure 5).

3. These teachers taught students in training schools who did not have strong academic backgrounds. Thus, they were concentrating on teaching "skills". However, they realized that there needed to be a better way to bridge the gap between their normal lecture/demonstration format and the computerassisted- design environment (CAD) for which they were trying to prepare their students. The opportunity to use software like Calques 3D gave them the possibility to bridge this gap and provide their students a more powerful way of visualizing and manipulating 3D objects in 2D, thus better preparing them for a CAD environment. Using the forms helped all of us to see how they could restructure their "modus operandi" to incorporate this new tool.

4. Discussions of concepts related to understanding various parts of the form helped all of us clarify the way that students could view objects in different ways (for example as translucent, transparent, etc.). Thus, we could come to an agreement on vocabulary as well as identifying the advantages of presenting objects in different ways.

5. This, in turn, allowed the designers to re-design the software in order to take into account the ways that the teachers intended to use the system. Without the use of the forms we would not have been able to obtain from the teachers the specifics of how they intended to use Calques 3D and in what ways they found it particularly attractive.

6. The description of the "Activities using software" provided a means for these teachers to formulate activities that were applicable to a wide range of teaching strategies. Moreover, this allowed us to impress upon them the need to concentrate on representing activities from the student's perspective. Otherwise we found that they became enamored with the software and tended to imagine a number of quite inventive uses that had very little pedagogical relevance. Moreover, most of these ideas were not grounded within the capabilities of Calques 3D and would not have been possible to implement .

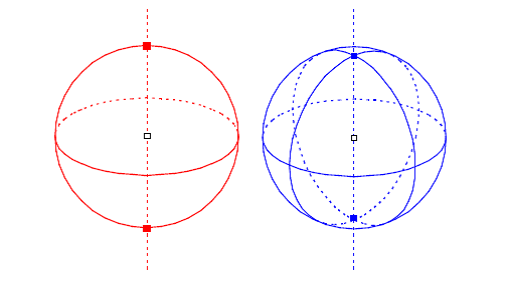
Figure 5

The 'wrongly placed' poles of a sphere and the correct ones

Figure 5

The 'wrongly placed' poles of a sphere and the correct ones

Among the problems we experienced were the following:

1. As noted previously there was a misunderstanding of the purpose of the forms. This was an easy problem to correct but it points to the more general problem observed in many Knowledge Acquisition scenarios, which is that it is necessary to reach a concensus on the objectives in order that the teachers and software designers better understand each other. Moreover, it is difficult for teachers with little or no experience in using this specific type of software to predict what types of problems students will most likely encounter.

2. In addition to the general misunderstanding about the use of the form, there were several instances of different interpretations of specific words. For example, the teachers thought the world "manipulation" signified any movement of an object on the screen (interface level) but for the software designers "manipulation" meant the re-orientation of an object on the screen with the coordinates actually changed. From the designers point of view this means that extracting a sub-figure of a construction or changing the observer's point of view, even if these operations require user manipulation, are not considered as manipulation operations but translating an object in the geometrical universe does.

3. These teachers were used to focusing on skills acquisition. Thus, it was difficult at times for them to describe their teaching on a more general level as we were asking them to do in completing these forms. They had a certain number of topics to cover and a very strict progression of items to present for each topic. Getting them to visualize how they would use Calques 3D to provide a more powerful way for students to work with objects in space was a real challenge.

4. The teachers found it hard to forecast the difficulties that students might have in using the software without actually seeing the students work with it. Our goal was to have them envision this based on their previous teaching experience but this proved very difficult. This provided additional validation to our thesis that educational software design without an incremental construction with a workable prototype is meaningless.

5. Since we were interested in non computer-based as well as computer-based activities we tried to design the forms to capture both types of information. However, we underestimated the impact that experimenting with the prototype would have on the teachers. They immediately saw a number of intriguing possibilities for using it (good point!) but then found it extremely hard to describe how they would "mix and match" their non computer-based activities (lectures, demonstrations, etc.) with all the possibilities they perceived with the software. And it was this mix that we were interested in capturing so that we could find ways to better improve the design, as well as suggest more effective ways to integrate Calques 3D in their lessons..

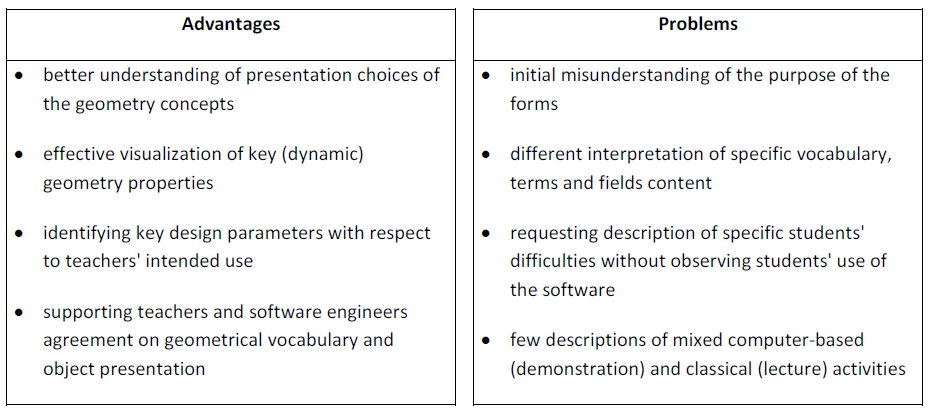
Table 1

Summary of advantages and problems experienced with the forms

Table 1

Summary of advantages and problems experienced with the forms

Table 1 summarizes the benefits gained from using these forms to capture "Teaching Knowledge" as well as the problems we encountered.

5. Conclusions and future work

1. The teachers believe that this software will provide them a way to bridge the gap between their traditional teaching methods and the Computer Assisted Design world for which they are preparing the students. Visualization and manipulation of 3D objects allows students to experiment with spatial properties (different views, translation, rotation, etc.) in ways that will have the most direct correlation with concepts they need for understanding CAD. We have noted this and should reemphasize it here along with a mention of how the feedback from the forms can help the software designer improve the software for the teachers use.

2. Teachers need the opportunity to experiment with this software in order to grasp its potential. As a part of that process it is important to have them explicitly describe how they will and will not use it. The forms allow us to capture their precise ideas and to re-structure the software so that it better suits their teaching needs. For example, specifying the types of student difficulties pointed out the need to include an on-line dictionary since students often do not know the meaning of terms.

3. Focusing the teachers attention on their teaching intentions and pedagogical objectives helped us to obtain specific suggestions for improving the software. Before developing and using the forms, there was a tendency for the teachers to request quite impractical and unrealistic software environments. Not only would these ideas have been almost impossible to implement but more importantly, they were not grounded in a pedagogical process of how they would be used.

4. Using the forms allowed us to discuss with the teachers their ideas about computer versus noncomputer based activities. In this way we obtained a much better idea of what features of the software would be particularly useful versus which features might be "nice to have" but not as pedagogically important. In this way we could concentrate on improving the features of the software that they deemed most important for their teaching goals.

5. As a side benefit we could use the information we collected from these teachers to train other teachers as to how to best integrate the use of Calques 3D with their usual approach to teaching this material.

Future Work :

1. We plan on testing the prototype in the classroom with the concomitant possibility of getting more feedback for improving the "ease-of-use" features of Calques 3D.

2. A project is planned to use the forms with geometry teachers in Scotland to observe if teachers describe their teaching knowledge in the same way. In particular we hope to ascertain where the forms are "culturally biased" versus what aspects seem more generally applicable to teaching dynamic geometry in different countries (or contexts). Another goal is to determine if the software is used in approach.

6. References

Acknowledgements

This work was done while the second author was an invited professor at the University of Nancy and LORIA in Spring 1998. Part of his support was from a Research Leave grant from Temple University. The dynamic geometry software design was supported by a grant from the "Region Lorraine".