Conception d’un environnement d’apprentissage adaptable: une étude en géométrie dans l’espace
N. Van Labeke , P. Bernat
Abstract
Un environnement informatique d'apprentissage doit pouvoir s'adapter à différents styles d'enseignement pour être effectivement intégré dans les classes et accepté par les enseignants. Nous pensons que les difficultés d'une telle adaptation proviennent de la diversité des points de vue sur chaque connaissance du domaine. Dans cet article, nous décrivons plusieurs exemples de cette diversité à différents niveaux de connaissances pour l'environnement de géométrie dynamique 3D que nous avons développé. A la suite d'une collaboration avec des enseignants, nous nous sommes particulièrement intéressés au cadre d'expression des informations collectées auprès d'eux, favorisant l'adaptabilité du logiciel aux diverses activités qu'ils souhaitent réaliser. La méthodologie de conception, décrite dans cet article, est basée sur la construction d'une ontologie de l'enseignement de la géométrie, déduite de contextes d'utilisation. Nous montrerons l’intérêt de cette spécification pour paramétrer un environnement selon des objectifs pédagogiques.
1. Introduction
Les recherches en EIAO ont conduit à la réalisation de logiciels pédagogiques qui quittent rarement les laboratoires où ils ont été conçus. Nous avançons l'hypothèse que les logiciels pédagogiques sont peu utilisés car non acceptés par les enseignants, non seulement parce que les enseignants les connaissent mal, mais aussi parce qu'ils ne correspondent pas à la représentation qu'ont les enseignants du domaine enseigné. Souvent, les tutoriels intelligents enseignent selon une stratégie spécifique et déterminée . Nous pouvons comparer l'usage d'un logiciel à celui du manuel scolaire. L'enseignant choisit souvent la progression de son cours indépendamment de la progression suggérée par les auteurs d'un manuel. Il choisit les exercices proposés à ses élèves en les adaptant si nécessaire.
Les enseignants considèrent l'outil informatique comme un assistant qui permet de préparer et de gérer les activités d'apprentissage, tout en conservant leurs propres choix de gestion. Ils ont souvent été associés comme auteurs au développement des EIAO et leur prise en compte, en tant que prescripteur, apparaît plus récemment dans plusieurs recherches. Dans le système ROBOTEACH de P. Leroux , l'enseignant peut créer des sessions pédagogiques en adéquation avec ses objectifs. La nécessité de permettre l'adaptation des styles d'enseignement a été remarquée également par N. Major qui propose dans COCA de définir des connaissances stratégiques paramétrables par l'enseignant . Dans CABRI , l'enseignant peut paramétrer l'interface en reconfigurant les menus.
Il est symptomatique de noter que les logiciels les plus utilisés dans l'enseignement de mathématiques dans les lycées et les collèges sont des environnements ouverts tels que les logiciels de géométrie dynamique ou des micro-mondes. Mais ouverture n'est pas synonyme d'adéquation automatique à l'enseignement. Il est nécessaire de réduire la distance entre les connaissances du micro-monde et celles à enseigner. En géométrie LOGO , un cercle est une courbe à rayon de courbure constant alors qu’en géométrie euclidienne il est défini par un centre et un rayon. La nécessité d'adapter la géométrie LOGO à l'enseignement "officiel" a conduit à la réalisation du logiciel EUCLIDE dans lequel les auteurs ont redéfini la syntaxe LOGO afin d'adapter son vocabulaire et ses fonctions.
L'adaptation du logiciel peut se faire au travers d'un langage de programmation ou au travers d'une interface spécialisée. C'est dans ce cas au concepteur du système d'anticiper les besoins didactiques des enseignants et de mettre à leur disposition les outils nécessaires à l'expression de ces besoins. Une telle anticipation est concevable dans le domaine de la géométrie plane, où la diversité des besoins est relativement réduite. Elle a été mise en oeuvre dans plusieurs logiciels de géométrie dynamique plane, tels que CABRI , CALQUES , Geometer's Sketchpad . Pour la géométrie dans l'espace (ou géométrie 3D), la situation est plus complexe notamment parce que la distance entre la restitution plane d'un objet et cet objet lui-même est importante. Cette restitution est sujette à de nombreuses interprétations pour lesquelles chaque enseignant s’efforce de trouver des approches pédagogiques adéquates. Plutôt que chercher à anticiper les besoins de chaque enseignant, les concepteurs doivent alors trouver un formalisme pour que les enseignants explicitent les différentes situations pédagogiques et les adaptent selon leurs besoins.
2. Interprétations multiples par niveaux de connaissances
Le travail coopératif avec des enseignants de géométrie en vue de la spécification d'un environnement informatique, fait apparaître la difficulté d'aboutir à un consensus sur la définition des objets du domaine et des fonctions opérant sur ces objets. Ces difficultés proviennent surtout de la multiplicité des pédagogies et des points de vues propres à chaque enseignant sur les attentes d’un tel environnement et de l'empêchement d'adapter certains points de vue à un environnement informatique. Nous montrons que ces problèmes, qui vont de la théorie à implémentation, se répartissent facilement dans le modèle de connaissances en quatre niveaux défini dans .
2.1. Le modèle de connaissances
En agissant sur des objets perceptibles au niveau de l'interface d'un EIAO, l'utilisateur agit indirectement sur une présentation externe des objets du domaine concerné par l'apprentissage alors que le système réagit sur une représentation interne qui ne lui est pas nécessairement isomorphe. Il convient donc de séparer clairement l'outil de spécification du domaine avec celui de l'interface.
Le niveau du Domaine est un niveau théorique représentant les connaissances expertes à manipuler et à enseigner de manière indépendante de tout concept informatique. Le niveau de Représentation correspond à une réalisation unifiée des éléments du domaine. Cette réalisation utilise des choix de l’auteur relatifs à la représentation des connaissances et met en évidence leurs relations. Les connaissances représentées sont réifiées au niveau de Présentation qui correspond ainsi à la modélisation des points de vue externes des objets du domaine perceptibles par l’utilisateur et proposés par l’enseignant prescripteur. Enfin, le niveau Visuel est le niveau de l’interface graphique utilisée par l’informaticien. Il dépend de la plate-forme de développement pour traduire la manipulation directe.
2.2. Le domaine : l’enseignement de la géométrie dans l’espace
La géométrie enseignée est une transposition de la théorie, variable au regard de la nécessaire progression dans l'acquisition des connaissances. Un même concept peut avoir des interprétations différentes. Ainsi, le concept de triangle varie selon l'usage que l'on veut en faire : un triangle peut être, soit un ensemble de trois points et/ou de trois segments, soit une région du plan; les côtés d'un triangle sont selon le cas des segments ou des droites. L'enseignement d’un même élément peut se faire selon des registres différents, selon des pédagogies différentes.
Il est tentant d'introduire toutes ces connaissances dans un logiciel afin de le rendre le plus complet possible. La géométrie hyperbolique peut facilement se modéliser sous un environnement de géométrie dynamique . La version 2.2 de CALQUES permet d’aborder la géométrie fractale. Sketchpad et CABRI autorisent la géométrie du quadrillage. Ces logiciels permettent également l’étude de la géométrie analytique. Dans CABRI II, les coniques et leurs équations font partie intégrante de l’environnement. On peut se féliciter de voir les barrières entre géométrie et analyse s’effacer aussi facilement, mais une telle confusion n’est pas sans poser des problèmes épistémologiques. Disposer d’outils analytiques rend possible la construction de certaines figures qui serait impossible avec le seul usage de la règle et du compas (par exemple la trisection d’un angle).
2.3. La représentation unifiée
Le niveau Représentation met en oeuvre une réalisation informatique unique des objets et des fonctions du domaine. Il met en évidence une facette conceptuelle unique qui définit et représente les propriétés d'un objet Il s’avère que cette transposition informatique peut aussi bien enrichir le modèle théorique que, au contraire, l’altérer de manière relativement importante .
En géométrie, l'utilisation d'un outil informatique interactif enrichit l'enseignement notamment par l'aspect dynamique qu'il introduit : on parle alors de géométrie dynamique. Face aux difficultés de visualisation et d’assimilation d’une figure dans l’espace, pouvoir la déformer (caractéristique forte des systèmes de géométrie dynamique) ou modifier la position de l’observateur pour la visionner sous un autre point de vue s’avèrent être des capacités permettant une meilleure assimilation de l’espace par l’élève à travers des activités facilitant son appropriation. Par contre, certains aspects de cette dynamique peuvent entraîner des effets de bord indésirables ou incompréhensibles pour un utilisateur non averti.
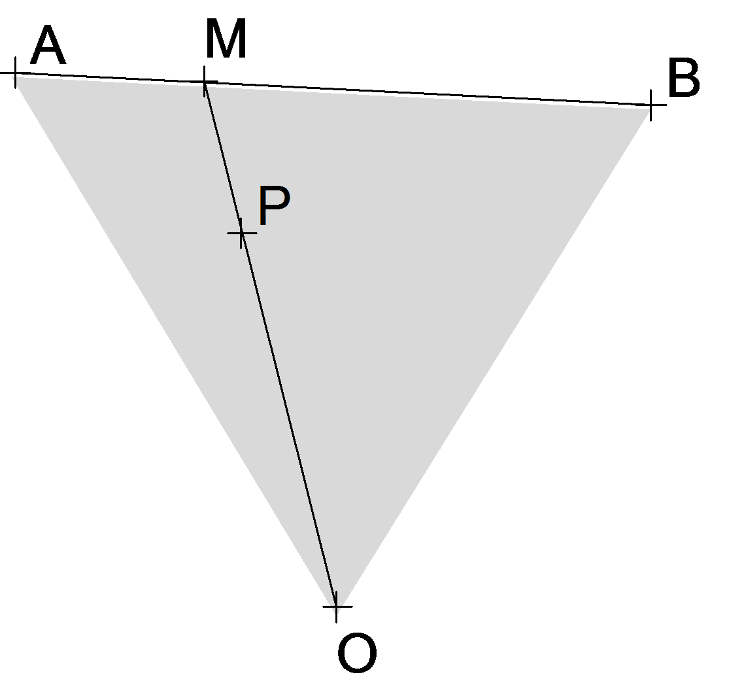
Dans l’exemple qui suit, nous allons voir que le résultat théorique attendu diffère nettement du résultat obtenu par les logiciels de géométrie dynamique. Soit un segment [AB], un point M sur [AB] et un point O hors de (AB). On crée enfin un point P sur [OM]. Quel est le lieu du point P lorsque M varie sur [AB] ? En théorie, ce lieu est l'intérieur du triangle (OAB) (Figure 1). Le tracé automatique du lieu est au contraire un segment de droite, car le rapport OP/OM reste constant lorsque M parcourt le segment [AB] (Figure 2).
2.4. La présentation des points de vue
Le niveau Présentation est une facette d'interface qui contient les vues multiples du même objet. Le niveau de présentation est le niveau où les enseignants vont exprimer leurs choix didactiques : du choix d'une présentation d'une connaissance dépend la situation d'enseignement induite par l'utilisation du logiciel. Ces choix nécessitent donc une analyse didactique. Un choix imposé par le concepteur d'un EIAO, s'il ne peut être remis en cause par les enseignants, sera critiqué. A titre d'exemple, S. Hocquenghem (cité dans ) regrette le manque de précision dans les projets didactiques de logiciels de géométrie dynamique à propos d'un choix d'interaction : faut-il créer l’intersection de deux droites variables dont les valeurs sont parallèles ? Les auteurs ont choisi de respecter un principe général d'interface (réaction du logiciel conforme aux attentes de l'utilisateur ) : ils interdisent de créer un point qui n'existe pas, même temporairement. Les choix de présentation, dans le cas d'un environnement de géométrie 3D, peuvent être des choix globaux de présentation (perspective, repère...), des choix de présentation spécifiques à chaque classe d'objets (solide, fil de fer...) et des choix de mode d'interaction (modes de déplacement des objets, rétroactions...). Nous détaillons quelques-uns de ces points dans les paragraphes suivants.
2.4.1. Choix globaux de présentation
Les éléments visuels de compréhension doivent faciliter la lecture d'une scène. Ils diffèrent des concepts du domaine à enseigner et peuvent exister dans d'autres domaines que la géométrie (légende, date, etc.) En géométrie, l'interprétation de la projection plane d'une figure dans l'espace constitue une difficulté majeure. Pour comprendre la position d'un objet dans une scène, nous introduisons des éléments visuels de compréhension, tels qu'un repère ou des plans de référence. Le choix d'un repère peut être réfuté dans certains contextes car le repère, en tant que concept géométrique, n’est pas abordé dans l’enseignement de la géométrie dans l’espace avant la classe de Terminale. D’autres propositions peuvent être envisagées telles que l'utilisation de plans ("cloisons") délimitant l'univers (Figure 3).
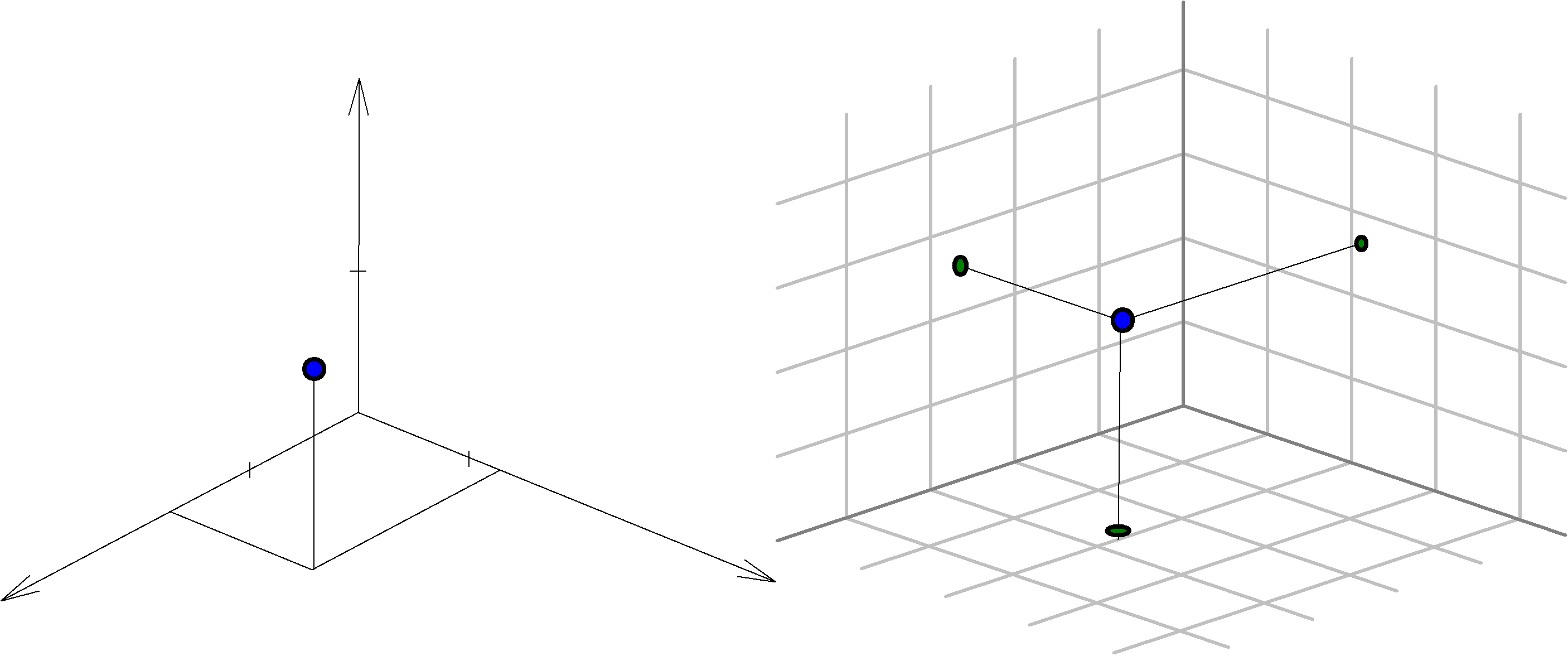

Figure 3
Deux exemples d’éléments visuels de compréhension. à gauche un repère ; à droite, l’utilisation des cloisons.
Le choix de tel ou tel élément visuel de compréhension dépend fortement du contexte et du niveau de connaissance de l'utilisateur. Par exemple, ces éléments sont inutiles dans le contexte de la géométrie du solide (constructions sur la base d'un solide comme le cube ou la sphère), où la présence d'un objet à forte connotation culturelle peut suffire à elle seule à fournir une bonne compréhension de l’espace. Des éléments visuels tels que les cloisons, utiles en début d'apprentissage de la géométrie dans l'espace, pourront être progressivement abandonnés.
2.4.2. Choix de présentation spécifiques
Le choix de la présentation des objets géométriques dépend également du contexte d'utilisation : la situation didactique que l'enseignant veut mettre en oeuvre. Le cube peut avoir plusieurs présentations possibles telles que le cube "fil de fer" dont toutes les arêtes sont dessinées ou le cube "faces cachées" dont les arêtes cachées ne sont pas dessinées. La présentation "faces cachées" du cube trouve son intérêt dans une géométrie du solide : elle fait apparaître le cube comme un objet physique qui a un volume alors que la présentation "fil de fer" met davantage en évidence les propriétés géométriques du cube (par exemple le parallélisme d'arêtes opposées). Un problème analogue se pose pour le choix de la présentation d’un plan. Faut-il réifier un plan en visualisant un rectangle contenu dans ce plan (quel rectangle choisir, n'y a-t-il pas risque d'induire une conception erronée du plan en limitant ainsi ses dimensions) ? Ne vaut-il pas mieux adapter chaque présentation du plan au contexte global de présentation comme dans la Figure 4 ? Cette question ne saurait admettre une réponse unique. Le choix définitif de présentation dépend de l'enseignant qui est le plus apte à juger de la pertinence de telle ou telle solution.
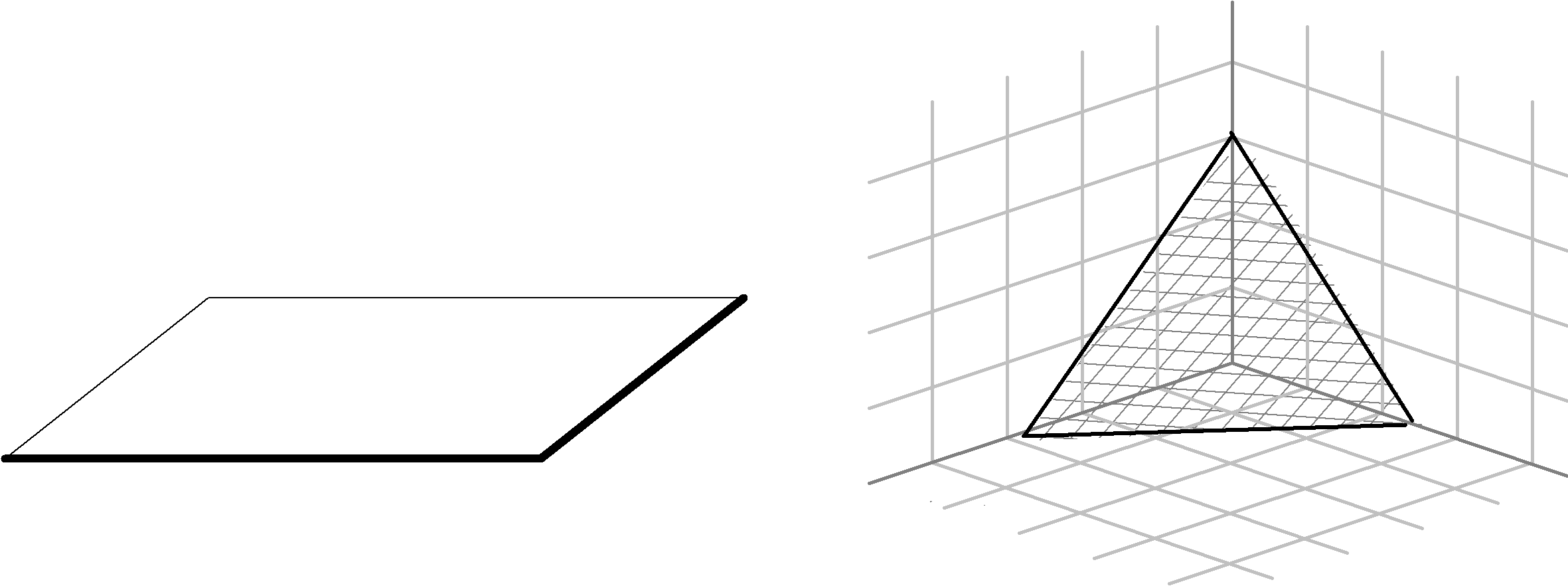

Figure 4
A gauche, la présentation “ classique ” d’un plan dans l’espace. A droite, la présentation d’un plan en tenant compte des cloisons.
2.4.3. Choix de modes d'interaction
L'interaction est une action, suivie d'une rétroaction immédiate au niveau de l'utilisateur et d'une réaction du système. Par exemple, la manipulation directe d'un point est l'une des actions essentielles en géométrie dynamique. Le déplacement d'un point selon les trois dimensions de l'espace ne peut s'effectuer par le simple déplacement de la souris dans un espace à deux dimensions. Pour restituer la troisième dimension, il devient indispensable de définir une action plus complexe (combiner le déplacement de la souris avec l'appui sur une touche du clavier, par exemple). La rétroaction doit alors indiquer clairement quel type d'action est engagée. Le point doit ensuite se déplacer conformément aux attentes de l'utilisateur : un déplacement de la souris doit entraîner un déplacement semblable du curseur et le déplacement du point dans l'espace doit "suivre" le déplacement du curseur sur l'écran.
Dans l’environnement de géométrie CABRI 3D, la solution choisie consiste à décomposer le déplacement d’un point sur un plan horizontal puis sur une droite verticale (modification de la cote du point) . Une autre méthode, utilisant les cloisons comme éléments visuels de compréhension (cf. §2.4.1), consiste à déplacer les points en manipulant directement leurs projections sur ces éléments (Figure 3). Quelle que soit la méthode choisie pour la manipulation directe, il est nécessaire de décomposer les mouvements dans l’espace en une série de mouvements dans des plans pour éviter les ambiguïtés ergonomiques. Une telle décomposition peut également présenter un intérêt pédagogique.
2.5. La visualisation des objets
Au niveau Visuel, on traduit à l'interface graphique les différents attributs des présentations des objets en accord avec les propriétés définies dans ces présentations. Il peut s’agir de la forme d’un point (rond, croix,...) et de sa taille, de l’épaisseur d’une droite, de la couleur par défaut de l’objet, ...
Ce niveau permet de définir le vocabulaire utilisé pour communiquer : messages d'aide, vocabulaire des menus, des boîtes de dialogue, etc. Les enseignants sont très exigeants vis à vis de la syntaxe. Ils n'admettent pas ce qu'ils considèrent comme une erreur de notation : un segment se note [AB] et non [A,B] et surtout pas AB, cette dernière notation étant réservée aux longueurs. Pourtant, cette syntaxe n'est pas figée : d'anciens manuels de géométrie utilisaient couramment des notations en contradiction avec les usages actuels. Ces notations diffèrent aussi selon les pays. Certains choix doivent donc être accessibles à ce niveau.
2.6. Vers un formalisme d'expression des activités
La conception d'un EIAO passe nécessairement par une collaboration entre individus issus de milieux divers (didacticiens, psychologues, informaticiens et surtout enseignants de géométrie) et nécessite l'utilisation d'un langage commun compréhensible par tous. En ce sens, la spécification se fait à niveau connaissance . Exprimer un modèle à niveau connaissance consiste à utiliser un langage de haut niveau plus facile à comprendre par une large communauté d'individus et indépendant d'un quelconque codage au niveau symbolique. Pour les enseignants impliqués dans le projet et les enseignants prescripteurs, ce langage doit faciliter l’expression de leurs choix de présentation des connaissances et des activités qu’ils veulent organiser autour de ces connaissances. Les ontologies fournissent un cadre suffisamment souple et intelligible pour une telle formalisation. Le paragraphe suivante présente l’état actuel de nos réflexion quant à l’utilisation de ce formalisme.
3. Des ontologies pour la spécification et l'adaptabilité d'un EIAO
Une base de connaissances établie à ce niveau de langage est une ontologie, c'est-à-dire une spécification explicite d'une vue abstraite et simplifiée d'un monde que l'on doit se représenter pour un certain usage . Elle est composée d'objets regroupés en classes, de fonctions, de relations. Aux entités de l'univers à modéliser, elle associe un texte lisible décrivant la sémantique des objets, celle des fonctions et celle des relations. Les ontologies ont été utilisées par Gruber pour gérer le partage et la réutilisation de connaissances expertes et plus récemment, pour gérer des connaissances pédagogiques .
Les ontologies constituent une librairie qui peut être consultée par les enseignants afin d'en extraire les éléments pertinents pour leur pédagogie : les connaissances du domaine, celles utiles à l'usage de l'application tels que les éléments de compréhension ou l'aide. Ils pourront, en utilisant ce formalisme, spécifier la configuration de l'environnement la mieux adaptée à la situation didactique qu'ils désirent mettre en place.
3.1. Construction d'une ontologie
La présentation d'un objet et les actions que l'on peut engager dépendent du contexte dans lequel cet objet sera utilisé. Nous rejoignons ici l'un des principes retenu par les auteurs du projet KACTUS : Le contexte peut être considéré comme un "point de vue" sur l'objet. Il est impossible d'énumérer par avance tous les points de vue que l'on peut avoir sur une classe d'objets. Nous définissons un contexte d'utilisation comme un cadre d'informations nécessaires à la réalisation d'activités partageant un objectif commun. A partir de cet objectif et en se basant sur des activités de référence, il est possible de définir les classes d'objets caractéristiques du contexte et leur présentation, ainsi que les fonctions disponibles à l'utilisateur final.
L'ontologie se construit incrémentalement à partir de chaque contexte en spécifiant les termes nouveaux qui apparaissent dans le contexte : nouvelles fonctions, nouvelles classes d'objets. Chaque nouvel élément s'ajoute à l'ontologie qui est finalement composée des contextes et de tous les termes utilisés dans les contextes et dans les spécifications des termes.
Seuls les enseignants auteurs directement impliqués dans le projet ont la possibilité d'étendre l'ontologie en définissant de nouveaux termes ou en enrichissant les objets, fonctions et relations nécessaires lors de la construction ultérieure de contextes : on parle alors de construction incrémentale. Les autres enseignants prescripteurs ont uniquement la possibilité de définir de nouveaux contextes en utilisant les termes existants : on parle alors d'adaptabilité.
Le développeur informaticien utilise cette ontologie pour implémenter le logiciel. Il connaît les objets et les fonctions nécessaires à la réalisation. Il choisit un formalisme d'implantation (par exemple une représentation objet) et doit compléter les spécifications à niveau connaissance par des spécifications de plus bas niveau (éléments d'interface, traduction visuelle des propriétés,...).
3.2. Exemple
Pour illustrer la méthodologie de construction de l'ontologie à partir d'un contexte, considérons l'exemple suivant (Figure 5) qui traite d’activités de construction de sections d’un cube donné par un plan.
En classe de seconde, les enseignants de mathématiques utilisent fréquemment un fascicule d'exercices intitulé "Dessiner l'Espace" . L'objectif de ce fascicule est de mener les élèves à une compréhension des objets et propriétés de la géométrie dans l'espace au travers d'activités de dessin en perpective cavalière. Les enseignants associés au projet ont retenu certains exercices du fascicule comme caractéristiques du contexte "Section du cube - Exercices". Ils ont précisé l'objectif de ce contexte et donné les caractéristiques qui, à leur avis, satisfont cet objectif.
Pour ces activités, des présentations particulières des classes d’objets cube et plan ont ainsi émergé. Le cube donné peut être présenté en mode "fil de fer" ou en traçant les arêtes cachées en pointillé. Par contre, la présentation "faces cachées" du cube (cf. § 2.4.2) n'est pas autorisée dans ce contexte : cette présentation ne permet pas en effet de visualiser les constructions demandées par ce type d’activités. Un plan est présenté en traçant ses intersections avec une instance correspondant au cube donné (notée #Cube0). Les facettes sont ces présentations particulières des classes d’objets cube et plan et leur usage est signalé dans la section "Classes d'objets" du contexte. Ceci conduit donc à surcharger les classes "Cube" et "Plan" par la spécification de ces facettes (voir Figure 6 pour la classe "Cube"). Seules les facettes explicitées dans un contexte sont autorisées pour un objet donné. Du fait de la construction incrémentale de l'ontologie, il n'est en effet pas possible d'anticiper sur toutes les facettes pouvant être définis ultérieurement.
Les fonctions disponibles à l'utilisateur sont énumérées dans la section "Fonctions" du contexte. Si elles ne sont pas spécifiées, il convient alors de les définir et de compléter ainsi l'ontologie. Le terme "Construire le Milieu", utilisé dans le contexte de la Figure 5, conduit à spécifier formellement la fonction "Construire Milieu" en précisant son arité et le type de ses arguments (Figure 7). La définition de la fonction fait intervenir les termes "Point" et "Segment" qui doivent également être définis en tant que classes d’objets.
3.3. Adaptabilité
L'enseignant prescripteur s'intéresse à la réification des objets du domaine (comment présenter un plan ?) et aux modes d'interaction. Les activités citées dans un contexte sont des activités de référence. Elle ont été proposées par les enseignants auteurs, comme exemples représentatifs du contexte d'activités. Tout enseignant prescripteur peut consulter la librairie ainsi constituée et choisir le contexte le mieux adapté à une activité qu'il veut proposer. Nous disons qu'il a la possibilité de réaliser une activité dans un contexte donné. Il s'agit bien alors de transcrire l'activité choisie en terme de paramètres destinés à l'exécution de l'application.
Jusqu'à présent, l'adaptabilité d'un logiciel aux besoins spécifiques de chaque utilisateur se fait couramment au niveau de l'interface. Ainsi, le logiciel CABRI permet de configurer l'ensemble des fonctions disponibles en manipulant directement les items des menus. Dans CALQUES 2 , il est possible de choisir différents modes d'interaction en cochant certaines cases dans une boîte de dialogue. Un tel paramétrage ne peut plus se concevoir dans le cas d'un logiciel trop complexe. Nous avons vu que dans le cas d'un environnement de géométrie 3D, les points de vue (et donc les paramètres) sont extrêmement nombreux et souvent dépendants les uns des autres. Les contextes d'utilisation définissent un ensemble de paramètres cohérents au vu de l'objectif du contexte. Le choix d'un contexte peut se faire par une opération unique qui induit automatiquement le choix de l'ensemble des paramètres. L'application ou agent système utilise les informations du contexte pour paramétrer le logiciel selon l'usage prescrit par l'enseignant. Il réalise automatiquement cette adaptation.
3.4. Implémentation
A l'occasion du développement d'un environnement de géométrie dynamique dans l'espace, nous avons réuni des enseignants et des didacticiens afin d'élaborer une ontologie d’un tel enseignement. Une partie des résultats est formalisée dans les paragraphes précédents. Pour faciliter la construction et la lecture ultérieure de cette ontologie, nous avons choisi de la présenter sous la forme d'un hypertexte. Chaque terme utilisé dans un contexte renvoie à une spécification ou constitue un terme primitif défini au sein de l'unité considérée. Il est alors facile de vérifier visuellement le degré de finalisation de l'ontologie : tous les termes utilisés ont été définis. Ce qui est différent de la complétude de l'ontologie puisque son développement incrémental présuppose qu'elle n'est jamais atteinte. Pour s'assurer de la cohérence de l'ontologie, il faudrait disposer d'un outil capable de vérifier si toutes les occurrences d'un terme aboutissent bien à une définition unique. Une réalisation est en cours de développement sous la forme de pages HTML.
4. Conclusion
Le formalisme des ontologies nous semble particulièrement bien adapté pour exprimer les choix pédagogiques. Il facilite la compréhension et l'adhésion des différents agents participant au développement du système. Des travaux ultérieurs devraient nous permettre de déterminer dans quelle mesure cette formalisation des connaissances sera réutilisable et s'appliquera dans le modèle en niveaux que nous proposons pour le développement d'EIAO.
Après avoir validé le cadre de description proposé et afin de permettre à l’enseignant prescripteur qui le souhaite de développer ses propres contextes, nous devrons mettre en place des outils de développement conviviaux. Nous devrons également étudier la mise en place d’outils permettant la vérification de la cohérence de l’ontologie. Alors, se posera la question de l’évaluation des ontologies. Nous nous demandons si l'ontologie développée est suffisamment riche pour permettre à tout prescripteur d’exprimer ses propres choix. Nous nous demandons aussi dans quelle mesure cette méthodologie est portable : la structure proposée pour définir les ontologies est-elle adaptée et suffisante pour exprimer les ontologies relevant d’autres domaines d’application ?
Dans le but d'y répondre, nous poursuivons les expérimentations sur le terrain.
Acknowledgments
Le présent projet bénéficie du soutien financier de la Région Lorraine et du Rectorat de l'Académie de Nancy-Metz.
Nous remercions Josette Morinet-Lambert pour sa relecture attentive et constructive.
5. Bibliographie
- Allard J.C., Pascal C. : EUCLIDE, un langage pour la géométrie plane, Cédic-Nathan, Paris, 1986
- Balacheff N. : Contribution de la didactique et de l'épistémologie aux recherches en EIAO en EIAO, in C. Bellissant (Ed.), Actes des XIIIe journées francophones de l'informatique, Grenoble, 1991, pp. 9-38
- Bernat P., CALQUES 2, Topiques Edition, Pont-à-Mousson, 1994
- Bernat P., Morinet-Lambert J. : Spécificités et modélisation de l'interaction dans un EIAO, Quatrièmes Journées EAIO de Cachan, Ed. Eyrolles, 1995, pp.208-220
- Abboud Blanchard M. : L'intégration de l'outil informatique à l'enseignement des mathématiques : symptômes d'un malaise, Thèse de l'Université Denis Diderot, Paris VII, 1994
- Goldenberg E.P., Cuoco, A. : What Is Dynamic Geometry? in Designing Learning Environments for Developing Understanding of Geometry and Space, Lehrer R. and Chazan D., eds. Hillsdale, NJ: Erlbaum. (to appear)
- Gruber T.R. : Toward Principles for the Design of Ontologies Used for Knowledge Sharing, International Journal of Human and Computer Studies, 43 (5/6), 1995, pp. 907-928
- Guin D. : Nécessité et richesse d'une interaction entre concepteurs des outils informatiques, didacticiens et formateurs dans l'enseignement des mathématiques, Apports de l'outil informatique à l'enseignement de la géométrie, Commission Inter-Irem Mathématiques et Informatique, 1994, pp. 5-16
- Jackiw N. : The Geometer's Sketchpad (version 3.0), Visual Geometry Project, Key curriculum Press, 1995
- Laborde J.M., Bellemain F. : Cabri Geometry II - Texas Instruments, Dallas, TX, 1994
- Laresgoiti-Anjewierden A., Bernaras A., Corera J., Schreiber T.H., Wielinga B.J. : Ontologies as vehicles for Reuse: a mini-experiment, KAW'96, 1996
- Leroux P., Vivet M. : De la modélisation d'un processus de coopération à la conception de systèmes coopérants d'apprentissage, ITS'96, LNCS 1086, 1996, pp. 197-206
- Major N., Reichgelt H. : COCA: A Shell for Intelligent Tutoring Systems, ITS' 92, LNCS 608, 1992, pp. 523-530
- Morlet C. : Dessiner l'Espace, IREM de Lorraine, Topiques Editions, 1989
- Murray T. : Having It All, Maybe: Design Trade-offs in ITS Authoring Tools, ITS'96, LNCS 1086, 1996, pp. 93-101
- Newell A. : The knowledge level, Artificial Intelligence, 18 (1), 1982, pp.87-127
- Nicaud J.F. : Modélisation du raisonnement algébrique humain et conception d'environnements informatiques pour l'enseignement de l'algèbre, Rapport pour l'obtention d'une habilitation à diriger des recherches, LRI, 1994
- Papert S. : Le Jaillissement de l'esprit. Flammarion, 1981
- Qasem S. : Cabri 3D : un environnement de géométrie dynamique dans l’espace, Séminaire de l’équipe Informatique et Formation, CRIN, 11/04/96
- Thibaut M.F. , Labarre R. : Some Hyperbolic Geometry with Cabri-géomètre, in Intelligent Learning Environments, the Case of Geometry, J.-M. Laborde (Ed)., ASI Series, F vol. 117, Springer Verlag, 1996, p. 218-230