Towards Student Modelling in Geometry with Inductive Logic Programming

Abstract

Using the TALC geometric tutor, a student can obtain a diagnosis about the correctness of his construction of a figure with respect to a teacher's specification. In the case his construction is incor¬rect, our aim is to improve the explanations given by TALC using a student (mis)conceptions model. Since the knowledge representation in TALC uses first-order logic, more precisely Horn clauses, our pur¬pose is to define and to exper¬iment with the use of Inductive Logic Programming (ILP) systems as a 'black box' in order to generate such geometric student model, using a corpus from didactic research about per-pendicular symmetry.

Introduction

The context of this paper is a tutor for the construction of geometric figures whose name is TALC (Desmoulins, 1994), a French acronym for Tutor of Logically Aided Construction. The aim of this tutor is to check the correctness of a student construction with respect to a teacher's specification. TALC is implemented in Prolog II+ and THINK C on the Macintosh platform. It uses Cabri-Géomètre (Bellemain & Laborde, 1995) as a server to construct figures. The diagnosis determines if the didactic contract (Desmoulins, 1993), on which the student and the teacher have come to an agreement with each other through the system, is satisfied. Each component of the contract could be considered as a degree of freedom that the system provides the teacher: the teacher's own text, the knowledge required to solve the problem, and the construction tools available by the system. The didactic contract is globally defined using first-order logic by $TIG \vdash S \Leftrightarrow F$, where F and S are, respectively, the translation of the student construction and the teacher specification, and where TIG is an axiomatic theory that defines the level of student ability required.

Three possible cases can be singled out of the diagnosis: the construction is correct, the construction is inadequate, and the construction is a particular case of the specification. In the last two cases, in order to verify the expression $TIG \vdash S \Leftrightarrow F$, one of its components can be modified: either the student creates another construction or the teacher changes his text or calls into question the knowledge he assumed the student possesses. Before modifying any component of the contract, it is preferable to generate explanations in order that the student accepts the diagnosis. A way to generate such explanations is to create a model of the student's geometrical (mis)conceptions. This model can be useful for adapting explanations for each student. Moreover, it provides the teacher with a more precise idea of the student's (mis)conceptions and a base to re-negotiate the contract. Based on the didactic hypothesis that the student's reasoning is consistent, our purpose is to use machine learning techniques to generate this model.

In the TALC system, generating a model of what the student believes in consists in looking for a theory TAG such that $TAG \vdash S \Leftrightarrow F$, for each couple (F, S) such that $TIG \nvdash S \Leftrightarrow F$, i.e., the construction is not correct. The representation of the geometric knowledge using Horn clauses within TALC leads us to the Inductive Logic Programming (ILP) paradigm.

This paper is organised as follows: Section 1 presents the principles and characteristics of Inductive Logic Programming and its utilisation for Student Modelling. Section 2 explains how ILP could be used to generate in TALC a model of what the student believes in. Finally, we describe in section 3 the experimentation we made with two systems that respond to TALC requirements. We present our first results on a body of misconceptions about perpendicular symmetry that stems from didactic research.

1. Using Inductive Logic Programming for Student Modelling

According to (Nicaud & Vivet, 1988), the more common methods for student modelling in Intelligent Tutoring Systems are :

• the overlay model where the student knowledge is a subset of the teacher's knowledge. The diagnosis is generated by comparing the respective knowledge of the student and teacher. The method is incomplete because only the lack of knowledge can be modelled. Both the systems GUIDON (Clancey, 1982) and WEST (Burton & Brown, 1982) use such a student model.
• the perturbation model where the expert knowledge is first encoded and then completed with the possible misconceptions of the student. These misconceptions (or bugs) represent perturbations of the expert model and are collected from observations and studies of student behaviour in a library. Many systems like PROUST (Johnson, 1983) or GEOMETRY TUTOR (Anderson et al., 1985) use bug libraries.

These two ways of student modelling start from a correct model, even if the knowledge representation and the perturbation method are different. On the other hand, some methods try to model behaviour, apart from its correctness. Those methods generally use machine learning techniques, such as the reconstructive diagnosis in the ACM system (Ohlsson & Langley, 1988). Starting from a decomposition of the problem, a set of primitives is defined. The diagnosis is reconstructive in the sense that it tries to describe observations with the aid of these primitives. In the ACM case, the student modelling consists in looking for 'solution paths' between the problem terms and its result in a search space created with such primitives. This path construction is created by learning from examples. The reconstructive diagnosis can be generalised by Inductive Logic Programming.

1.1. What is Inductive Logic Programming?

Inductive Logic Programming (ILP) can be defined as the intersection of Machine Learning and Logic Programming research areas. Thus the aim of ILP is to learn a definition (called hypothesis) of target concepts from observations, where the knowledge representation language is Horn clauses. The set of observations consists of positive examples $E^+$ and negative examples $E^-$ of these concepts. These examples usually are ground facts. The knowledge relative to the domain where the machine learning takes place is called the background knowledge $BK$. The set of Horn clauses representing $BK$ is either ground facts or non-ground rules.

The principle of Inductive Logic Programming is then as follows (Muggleton & De Raedt, 1994). Given a background knowledge $BK$, a set of positive examples $E^+$, a set of negative examples $E^-$, find a hypothesis $H$ such that the following conditions hold :

• completeness: $\quad BK, H \vdash E^+$
• consistency: $\quad BK, H \nvdash E^-$

The completeness condition requires that the hypothesis $H$ covers all positive examples. The consistency condition requires that $H$ does not cover any negative example. A third practical, but necessary condition, $BK \nvdash E^+$, has to be added to the previous ones. It checks that background knowledge does not yet hold any complete concept definition.

Taken as a whole, the induction process can be viewed as a search problem. Induction consists in exploring a search space containing all possible hypotheses in order to find one verifying completeness and consistency.

1.2. ILP Systems Characterisation

These general principles are currently implemented in many ILP systems. However, they are significantly different the one from the others. In order to select some well-adapted ILP systems to student modelling, we first extracted the main features characterising each ILP system. These characteristics concern the involved machine learning processes and the restrictions on both the representation language and the search space. They are the following :

• incremental or empirical learning : in a non incremental (empirical) ILP, the examples are given at the beginning and are not modified afterward, although in incremental ILP, they are given one by one by the user;
• interactive learning : in interactive ILP, the system is allowed to ask questions to the user (called "oracle") about the intended interpretation of an example or a clause. Obviously, interactiveness implies incrementality but can be involved in some phases of empirical learning like theory revision;
• single or multiple predicate learning : in single predicate learning, the observations are examples of only one concept. The aim of multiple predicate learning is to learn a set of possibly interrelated predicate definitions;
• theory revision : the theory revision usually consists in inductive learning starting from an initial approximation of the concept to induce.
• predicates invention: the ILP system is able to invent new predicate symbols, when the vocabulary of the background knowledge is insufficient to construct hypothesis;
• intentional or extensional background knowledge : an intentional background knowledge can contain both ground facts and non-ground clause, whereas an extensional one is represented with ground facts only;
• predicate instantiation mode : considering that the clauses are logic programs, instantiation mode allows the designations of predicate arguments as input or output.
• predicate typing: it constrains predicate arguments to take values only in a predefined set. Both these two previous characteristics are usually used to restrict the search space and come from the paradigm of Logic Programs Synthesis.

To conclude this section, we note that one of the major interest of ILP for student modelling is to be able to manage a set of example from the student behaviour, without concern about correctness (with respect to the reference knowledge). Another characteristic, predicates invention, is important because the student model could not only be expressed with the predicates of the reference model.

The first proposition to use ILP in student modelling is from Kawai (Kawai et al., 1986). He postulate that the student model can be represented with a set of Horn clauses. This proposition was applied in a more concrete way in the SARAH system (Siou, 1994), in order to re-educate aphasia. In this framework, the advantage of ILP is that it can reconstruct each aphasic person's own language model. These approaches are nowadays the only ones concerned with student modelling with ILP.

2. Inductive Logic Programming with respect to TALC

In this section, we first present how Inductive Logic Programming could be used with respect to TALC : we instantiate the different components of an ILP system in TALC. We then present an example of a student model we want to automatically learn with an ILP system.

2.1. Using ILP in TALC

In order to use ILP in the context of TALC, we need to describe how the different components of TALC are connected with the following components of an ILP system : the knowledge representation language, the observations of the target concepts and the background knowledge.

As said in the introduction, TALC provides three kind of diagnosis : the figure is correct, the figure is a particular case and the figure is inadequate (some geometrical properties or objects are missing). In this paper, we only deal with the case where some properties are missing in the student construction. Logically, it means that $TIG \nvdash F \Rightarrow S$. The knowledge representation language involved in TALC is LDL (Logical Description Language) in which the teacher specification and the student construction are translated before being compared. We do not need to transform it as it is a first-order language (without function symbols).

Defining the observations of the target concepts is not immediate. Our problem is to find a theory TAG such that $TAG \vdash F \Rightarrow S$, for each couple < figure, specification > (F,S). In terms of machine learning, the positive examples would be the set of expressions $F \Rightarrow S$. But it is unnecessary to look for a model of the whole student construction. Indeed, considering that a LDL formula is a conjunction of properties $(S = S_1 \cap S_2 \cap … \cap S_n)$, the diagnosis of TALC gives us the set of non proved properties $S_i$ within F, i.e. such that $TIG \nvdash F \Rightarrow S_i$. For incorrect constructions F, the properties of S could then be divided in two kinds : proved and non proved ones. Then we can take as positive examples every formula $F \Rightarrow S_i$ such that the property $S_i$ is not proved (notice that there is no negative example because TALC just considers the figures that the student has declared correct).

For example, if the following properties $symmetric([a b],l,[a' b'])$ and $square(p1,p2,p3,p4)$ are not proved within F, i.e. $TIG \nvdash F \Rightarrow symmetric([a b],l,[a' b'])$ and $TIG \nvdash F \Rightarrow square(p1,p2,p3,p4)$, each of the formulae $F \Rightarrow symmetric([a b],l,[a' b'])$ and $F \Rightarrow square(p1,p2,p3,p4)$ are positive examples to automatically induce both the target concepts symmetric and square.

Unfortunately, ILP systems do not accept such formulae as examples but only literals. In order to fix this problem, we could consider that the formula F belongs to the background knowledge (via the deduction theorem). The trouble is that the system loses the implication between F and S and is only able to learn a theory covering a single couple (F,S). Consequently, we adopt a standard solution which consists of renaming every object of the formula $F \Rightarrow S_i$ with different and unique names for each couple (F,S). For example, if the property $symmetric(s,l,s')$ of the specification S are non proved in both the constructions F1 and F2, then the positive examples could be respectively $symmetric(s1,l1,s1')$ and $symmetric(s2,l2,s2')$. The corresponding constructions F1 and F2 are renamed using the same substitution and added to the background knowledge.

The background knowledge BK is of course composed by the theory TIG and, as shown previously, by the renamed properties of the construction F.

Finally, we can identify the needs of TALC with respect to an ILP system from the characteristics enumerated in section 1.2.

Inductive Logic Programming process needs negative examples in order to constrain and guide the hypotheses search. Because such negative examples are not available from TALC, we think about asking the user to validate (for positive examples) or invalidate (for negative examples) some properties submitted by the system about a current construction. Interactiveness is then required. On the other hand, as we defined it previously, the learning process could be empirical (after, for example, each set of exercises) and incremental (after every diagnosis) equally. Only the problem of negative examples generation would then restrict our choice.

Because the TIG theory is a part of the background knowledge, we need to describe it intentionally. The search space can also be restricted by typing geometrical objects with ILP systems which provide this characteristic, but it is not necessary to have a predicate instantiation mode. Therefore, predicate invention, multiple predicate learning and theory revision could be useful but not necessarily essential. Only experimentation will determine it.

2.2. Example of student modelling with ILP

In their didactic research, Grenier (Grenier, 1988), concerning traditional paper and pencil work, and Tahri (Tahri, 1993), concerning work with computer software, identified a set of correct and incorrect student conceptions related to the perpendicular symmetry of a segment across a line. These conceptions are relevant examples of what could be automatically learned with an ILP system.

For example, the following conceptions are incorrect :

• the 'parallelism' conception where the student confuses perpendicular symmetry with the parallelism (figure 1.A).
• the 'perceptibly perpendicular-to-axis distances transfer' conception where the student builds a semiglobal construction (some objects of the construction are not linked to some others). In the case of figure 1.B, only the endpoint A' of the segment [A' B'] is correctly located at the intersection of the circle and the line (A A'). The endpoint B' is placed perceptibly on a line perpendicular to the axis Ax.

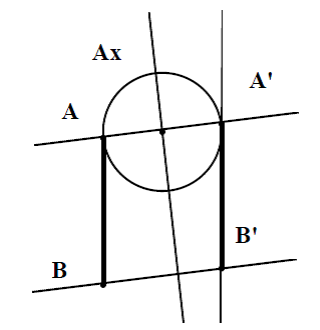
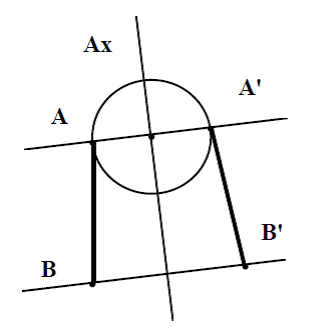
Figure 1

Incorrect concepts of perpendicular symmetric: (A) 'parallelism' and (B) 'perceptibly perpendicular-to-axis distances transfer'.

Figure 1

Incorrect concepts of perpendicular symmetric: (A) 'parallelism' and (B) 'perceptibly perpendicular-to-axis distances transfer'.

The aim of the exercise is to verify the comprehension by the student of the concept of perpendicular symmetry. We try here to obtain a definition of the target concept symmetric(S1,DR,S2) which means that "the segment S2 is the perpendicular symmetric of the segment S1 across the line DR". A positive example for both the previous figures is then symmetric([A B],Ax,[A' B']).

From these constructions and from a theory TIG required to solve this exercise, we would like for an ILP system to generate the following theory TAG1 related to the 'parallelism' concept :

        TAG1 = TIG ∪ symmetric([a b],d,[a' b']) ⇐
                    parallel([a b],[a' b'])
                    perpendicular([a a'],d)
                    perpendicular([b b'],d)
                    distance(a,d,d1)
                    distance(a',d,d2)
                    equal(d1,d2)
    

In this case, we suppose that each predicate involved in the definition of TAG1 still exists in the background knowledge.

The theory TAG2 is related to the 'perceptible' conception described above :

        TAG2 = TIG ∪ symmetric([a b],d,[a' b']) ⇐
                    distance(b,d,d3)
                    distance(b',d,d4)
                    almost-equal(d3,d4)
                    perpendicular([a a'],d)
                    perpendicular([b b'],d)
                    distance(a,d,d1)
                    distance(a',d,d2)
                    equal(d1,d2)
    

Generating the theory TAG2 needs the predicate invention technique in order to represent the fact that the distances between the axis Ax and each of the endpoints B and B' are approximately equal, i.e. the predicate almost-equal(d3,d4).

3. Experimentation

In this section, we describe an experimentation with ILP systems. We first present the two systems we select. We then make precise how the set of examples was defined. Finally, we present the first results obtained using these two systems on the concept of perpendicular symmetry.

3.1. Selected ILP systems.

In order to use an ILP system as a 'black box', we made a two-steps selection.

First we discard some systems because they were unavailable or not sufficiently documented, or because we did not have the required interpreter or development environment. After this selection, we were left with the four following systems: FOIL (Quinlan, 1990), FOCL (Pazzani & Kibbler, 1992), GOLEM (Muggleton & Feng, 1992) and CLINT (De Raedt, 1991), from twenty available candidates (or claimed available).

Secondly we compared them following the characteristics described in 2.1 with respect to TALC requirements. Interactive and incremental learning is certainly consistent with TALC requirements and lead to CLINT as the best choice. We also selected the FOCL system and we fixed the problem of negative examples by automatically generating them before each induction process. A brief description and a comparison of these four systems is presented in (Van Labeke, 1995).

3.2. Reference Body.

The examples come from the symmetric misconceptions studied by Grenier and Tahri and are described in section 2.2. We redefined the original texts in TALC by specifying, for each of them, the teacher specification S, the related geometrical theory TIG and the student construction F.

Induction of these concepts with ILP was carried out separately from the diagnosis in TALC: we recovered the LDL (Logical Description Language) translations of the components of each exercise (theory TIG and text S) and the corresponding student construction (figure F) and put them into each ILP system after some needed adaptations (syntactical modifications, constant and variable renaming, ...).

Although it is not its main goal, TALC can be used to propose to the students problems of geometrical construction. In this way, student understanding of perpendicular symmetric concepts could be checked. However, the actual TALC diagnosis cannot refer to any property but only to CDL properties (Classroom Description Language, the texts language), which are quite basic (membership, parallelism, equality, ...). In order to give to the teacher the ability to express high-level concepts, we suggest allowing him to write his own macro-definitions.

Formally, we define what a macro-definition is in the same manner as what a procedure is in a programming language: on the one hand we must define the semantics of a macro-definition declaration, and in the other hand the semantics of the utilisation of a macro-definition. A declaration of a macro-definition creates a new predicate (i.e. clarifies its name and its formal parameters) and associates it with a CDL text. An utilisation of a macro-definition replaces the predicate by the CDL text associated to it , binding the formal parameters by the effective ones.

For example, the macro-definitions which would define the midpoint of two points and the perpendicular symmetry of a segment across a line could be described using CDL language as follows ([A B] represents the segment A B, (A B) the line A B, |A B| the distance between A and B and ⊥ is the perpendicular relation) :

        MIDPOINT(I, A, B) :=
            I ∈ [A B],
            | I A | = | I B |.
        SYMMETRIC( [A B], L, [A' B']) :=
            MIDPOINT(I, A, A'),
            MIDPOINT(J, B, B'),
            I ∈ L,
            J ∈ L,
            (A A') ⊥ L,
            (B B') ⊥ L
    

A CDL text using this macro-definitions and describing the symmetric of a right triangle (A B C), could be the following:

        s1 = [A B],
        s2 = [B C],
        s3 = [AC],
        s1 !- S3,
        line(Ax),
        SYMMETRIC(s1, Ax, s11),
        SYMMETRIC(s2, Ax, s22),
        SYMMETRIC(s3, Ax, s33).
    

Since our corpus is about symmetry and obviously the corresponding predicate is not a CDL one, we need to use such macro-definitions. Because TALC does not yet provide this feature, it is then necessary to simulate it. For this purpose, we use a unique text only containing the definition of the target concept, i.e. the perpendicular symmetry of a segment across a line. Thus this text itself, with the following specification, is a macro-definition of the target concept SYMMETRIC([A B], L, [A' B']). :

        I ∈ [A A'],
        |I A| = |I A'|,
        J ∈ [B B'],
        | J B | = | J B' |,
        I ∈ L,
        J ∈ L,
        (A A') ⊥ L,
        (B B') ⊥ L
    

In the same way, the construction done by the student is considered as a positive example of the concept SYMMETRIC. Once more this underlines the need for additional knowledge as soon as additional functionalities are built.

3.2. Experimental Results

The first experiments focused on the concept of 'parallelism' (see figure 1.A) because the expected results were relatively simple. As shown in the previous section, the target predicate related to the concept of perpendicular symmetry cannot be expressed in TALC. Its introduction in the ILP systems required us to define both the predicate arguments and types. Since the LDL predicate describing a segment is as follows :

segment(s1,p1,p2,l)

the segment s1 is defined by its endpoints p1 and p2 and by its directed line l

we chose to define the target predicate with the segments and the symmetric axis identifiers:

symmetric(s1,ax,s2)

the segment s2 is symmetric to the segment s1 with respect to the axis ax

The experiments using the incremental learning system CLINT confirm the limits already observed during its evaluation: whatever way we modify the background knowledge or the definition of the target predicate, the induction process requires too much time and is unable to deal with more than the first submitted example. In this case, the process gives the following minimal hypothesis:

        symmetric(s1,ax,s2) :-
            segment(s1,p1,p2,l1),
            segment(s2,p3,p4,l2),
            line(ax).
    

In our opinion, these problems come from CLINT definition of high-order rules used in restricting the search space and from the recursive definition of the TIG axioms.

CLINT advantage is to be incremental and interactive. Nevertheless, with the current documentation, where only a formal description of these high-order rules is given but no practical method to adapt them to concrete problems, the use of CLINT as a black box did not appear well adapted to our purpose.

We focus then on FOCL, which is non-incremental. Unfortunately all negative examples should be explicitly given. This last limitation was overcome by generating them on each positive example independently. Results depend on learning parameters and on the use of the background knowledge. The nearest definition with regard to the didactic results is the following:

        symmetric(s1,ax,s2) :-
            segment(s1,p1,p2,l1),
            segment(s2,p3,p4,l2),
            par(l1,l2),
            perp(l3,ax).
    

Here we really obtain the property that s1 and s2 are two segments and that l1 and l2, their respective support lines, are parallel. However, there is no information about the rest, i.e., the perpendicularity between the axis Ax and both the lines (A A') and (B B'). The only literal about perpendicularity perp(l3,ax) is geometrically insufficient. According to Tahri's classification, this hypothesis is then acceptable.

Even if FOCL needs all negative examples before the learning process, this could be overcome in an interactive system by first generating all possible negative examples using the Closed Word Assumption and then asking the student whether each of them is valid or not.

Conclusion

Our purpose was to define and to experiment with the use of Inductive Logic Programming systems as 'black boxes' in order to generate a model of student beliefs in geometry.

We first selected, among ILP systems referenced in the literature, the ones which were really usable, i.e., were available, sufficiently documented and efficient. We also defined a qualitative characterisation of ILP systems that we used to choose suitable systems for the requirements of TALC. Our chief discriminating characteristic is the necessity to describe background theory intentionally, i.e., with both facts and rules. Then we performed experiments based on a body of examples chosen from didactic research about construction of the perpendicular symmetry of a segment. In particular, we tried to use ILP systems to induce the incorrect concept of 'parallelism'. The results of the FOCL system are adequate enough. However, the CLINT system could not overcome limitations due to the background knowledge size and the recursive form of the axioms.

One of the problems we had to tackle was that examples of the target concepts were in the form of implication formulae, although ILP systems require them as facts. We fixed this in a classical manner by introducing the left part of the implication as a set of facts in the background knowledge and by renaming every constants, in order to preserve the connection between these facts and the related observations (the right part of the implication).

This research revealed that some insufficiencies in the TALC system must be rectified in order to continue large-scale experimentation about other incorrect concepts (in vitro or in vivo). First, we need to obtain a more complete diagnosis. Secondly, we need to allow the teacher to define his own macro-definitions, in order to overcome the elementary expressiveness of the CDL primitives. These additional functionalities are currently implemented.

In a more practical view, the ILP systems requiring negative examples necessitate to ask student about the validity of potential ones. Without a doubt, this interactivity is not necessary because an ILP system we recently found requires only positive examples : LILP (Markov, 1995). More generally, our point of view about this 'black box' experimentation is that it is more suitable to design an adapted ILP component. Indeed, our requirements are really restricted compared with all the possibilities that an ILP system provides. Many libraries of ILP techniques exist and could be useful for that aim.

In conclusion, for the long term, an important issue is how to exploit the induced model. Firstly, the correctness of the induced TAG theory should be established. If the model is geometrically correct (for example when the student uses geometrical axioms or theorems that the teacher did not specify), it is possible to update the TIG theory with these axioms (with teacher agreement). On the contrary, it seems to be interesting to automatically generate a counter-example which allows pointing out the incorrectness of student understanding. Broadly speaking, we could provide the teacher a way to describe system reactions following misconceptions extracted from TAG analysis, i.e., to propose to the student an activity following conditions founded in the model.

Bibliography