Towards a Learner Modelling Engine for the Semantic Web

Abstract

We describe XLM, the learner modelling subsystem of LEACTIVEMATH, from the viewpoint of how it makes use of technologies associated with the Semantic Web. We discuss how a better usage of these technologies could make of XLM a more generic learner modelling engine to serve a variety of elearning systems. We try to foresee important issues to be addressed and difficult problems to be solved in the way to this goal.

1 Introduction

LEACTIVEMATH is a Web-based educational system for mathematics that employs some of the Semantic Web standards and technologies. To start with, it is a content-based system which uses OMDOC , a markup language for representing mathematical documents with emphasis in their meaning rather than in their appearance. LEACTIVEMATH content has metadata based on LOM with extensions to support the specific needs of LEACTIVEMATH components. Content can be presented in different formats on different devices by means of XSL . LEACTIVEMATH is developed using JAVA, a main programming language for web-based systems, and it uses the XML-RPC protocol to communicate with its remote components and associated systems. The learner modelling subsystem of LEACTIVEMATH, called the Extended Learner Model (XLM), was designed to deal with and benefit from the features of its host system. Nevertheless, it was expected to be easily detachable from LEACTIVEMATH to serve other but similar systems, either as an embedded component or by offering its services on the Web.

This paper first describes the current design and implementation of XLM from a Semantic Web perspective, digging into important issues of general relevance. Then it explores the possibility of accomplishing the goal of transforming XLM into a generic learner modelling engine for Semantic Web-based educational systems. Finally, some conclusions are proposed.

2 From Content to Learner Models

Figure 1 illustrates the process by which XLM gets information related to learner interaction with educational content. In essence, content encoded in OMDOC is transformed in a presentation language (HTML, MATHML or PDF) using style-sheets and VELOCITY . Some of the content items and their presentations allow learners to interact with them in a way that the interaction can be captured by LEACTIVEMATH and reported to XLM in the form of event messages containing basic data, such as identifiers for learners and content items and the type of event reported, and additional information such as (for some events) a measure of learner performance.

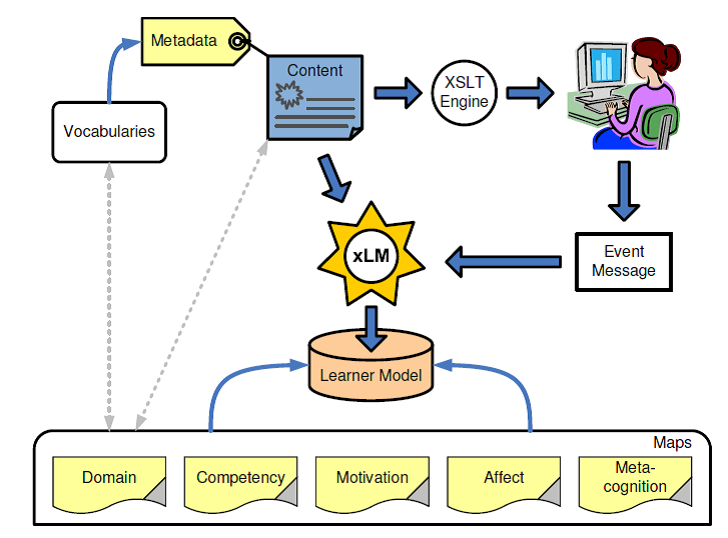
Fig. 1

The process by which content is transformed into information about learners to feed learner models in XLM. Thick arrows represent information flow whereas thin arrows speak of relationships between elements.

Fig. 1

The process by which content is transformed into information about learners to feed learner models in XLM. Thick arrows represent information flow whereas thin arrows speak of relationships between elements.

A variation of this scheme consists in the introduction of additional components acting as diagnosers of learner behaviour, which evaluate what happens along the interaction of learners with content and produce judgements on learners’ states and dispositions. Examples of such additional diagnosers include an assessment tool that produces judgements on learners’ levels of competency, a self-report tool through which learners emit judgements on their own affective states, and a situational model that produces judgements on learners’ motivational state. A further variation of the scheme consists in learners interacting with their learner models instead of interacting with educational content. The models are made available through an XLM component called OLM (for Open Learner Model) that provides learners with a graphical user interface to their models. It includes facilities for inspecting and challenging beliefs in the models and the evidence supporting them. OLM acts also as a diagnoser, producing judgements on learners’ levels of meta-cognition.

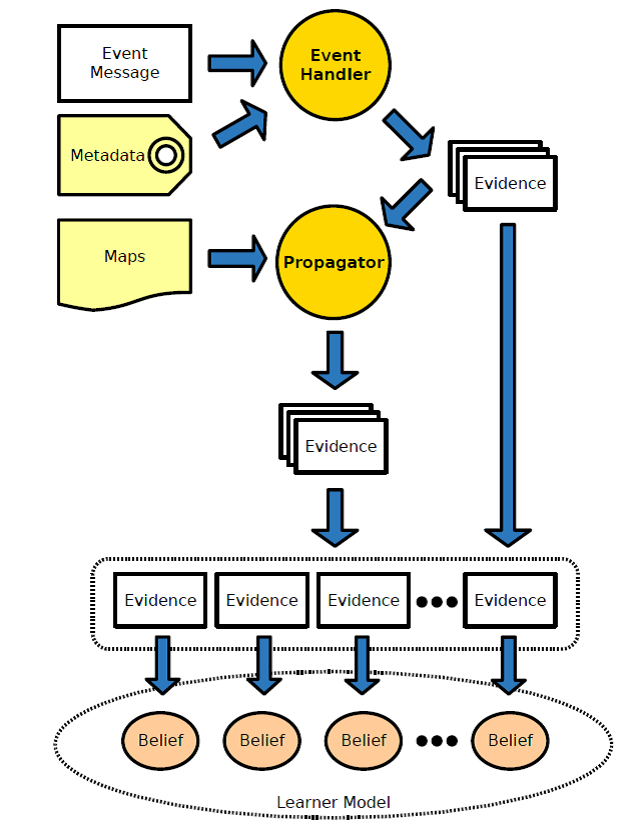
Fig. 2

The process of interpreting events to produce evidence for beliefs in learner models. Arrows represent information flow.

Fig. 2

The process of interpreting events to produce evidence for beliefs in learner models. Arrows represent information flow.

Once XLM receives an event message, it proceeds to interpret it using the event handler that corresponds to the type of event reported in the message (figure 2). The event handler uses the identifier for the content item, as reported in the message, to recover the item’s metadata that sets the context for interpreting the rest of the message. In particular, metadata provides information to identify the domain topics and competencies related to the event, while data in the message helps to identify related affective and motivational factors, if any. Armed with all this information, the event handler produces evidence to update a selection of beliefs in a learner model identified by their belief descriptor

(domain topic, misconception, competency, affective factor, motivational factor,metacognitive factor).

Each element in a belief descriptor must appear in the concept map that specifies the internal structure of the corresponding dimension in the learner models (bottom of figure 1). It is the composition of these maps in the predefined way (sketched in figure 3) what rules the composition of belief descriptors and defines the overall structure of learner models in XLM. The structure of the maps is used by propagators to spread the evidence produced by event handlers through the network of beliefs, producing in the end a relatively large collection of indirect evidence for a broader selection of beliefs. The final step in the process of learner modelling is updating the beliefs in a model on the light of the new evidence accumulated.

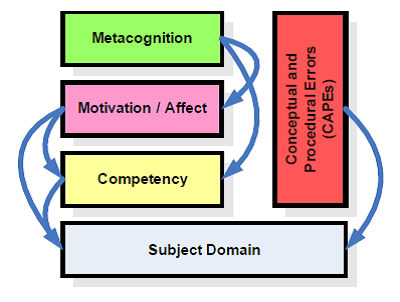
Fig. 3

The possible combinations of dimensions that define the structure of XLM learner models.

Fig. 3

The possible combinations of dimensions that define the structure of XLM learner models.

2.1 Example

To illustrate what has been explained above, let us consider the case of a learner that is studying Differential Calculus and has finished the exercise on differentiation of linear functions shown in figure 4.

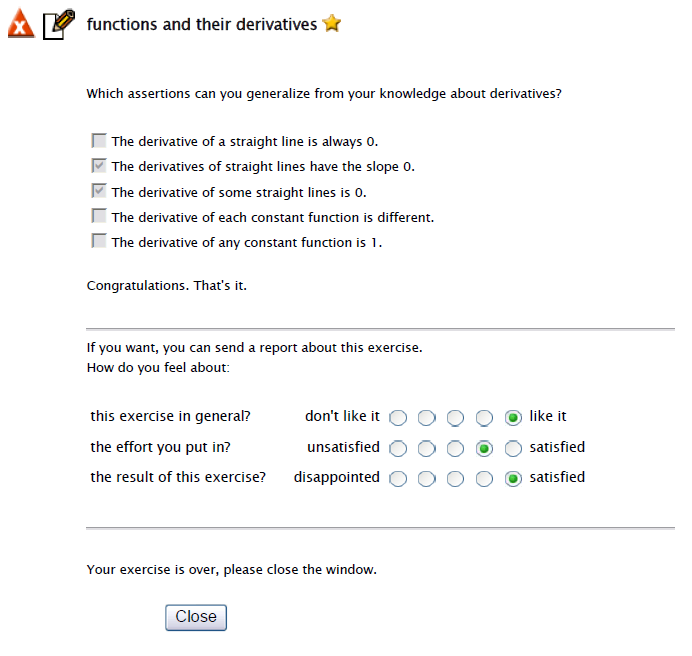
Fig. 4

Example of exercise and self-report tool in LEACTIVEMATH.

Fig. 4

Example of exercise and self-report tool in LEACTIVEMATH.

XLM receives an event message reporting that the learner has just finished successfully the exercise identified as mbase://LeAM_ calculus/exercisesDerivs/mcq_const_lin_derivs (success rate = 1.0). Then XLM requests the exercise metadata and receives the following information, among other:

• Exercise is for: ex_diff_const and ex_diff_lin.
• Difficulty: very easy.
• Competency: think mathematically.
• Competency level: simple conceptual.

Subsequently, XLM goes from the exercise to a pair of examples of differentiation of constant and linear functions (.../ex_diff_const and .../ex_diff_lin, respectively), to definitions of the corresponding differentiation rules, and so on up to the nodes diff_quotient, deriv_pt and derivative in the map of the subject domain, which stand for the domain topics of difference quotient, derivative at a point and derivative, respectively. Now XLM can construct the descriptors for the beliefs the exercise provides new evidence for:

• (diff_quotient,_,think,_,_,_),
• (deriv_pt,_,think,_,_,_) and
• (derivative,_,think,_,_,_).

These beliefs are all on the competency level of the learner to think mathematically on/with the topics trained or tested by the exercise. Information on the difficulty and competency level of the exercise and the success rate achieved by the learner is used to calculate probabilities for the learner being at any of four possible competency levels.

These probabilites are then transformed into a belief function , a numeric formalism for representing beliefs that generalises probabilities and allows for a better representation of ignorance and conflict. It is the formalism used by XLM to represent its beliefs and their supporting evidence .

The initial set of direct evidence (three pieces) is input to propagators which in this case produce twenty two new pieces of indirect evidence for beliefs with descriptors such as (differentiation,_,think,_,_,_), propagating on the domain map, and (derivative,_,judge,_,_,_), propagating on the competency map.

The learner’s self-report of their affective state (bottom of figure 4) would be delivered to XLM in another event message and then used to infer new evidence for beliefs on the affective dispositions of the learner towards domain topics and mathematical competencies, with descriptors such as (diff_quotient,_,_,liking,_,_) and (differentiation,_,think,affect,_,_).

3 Design and Implementation Issues

Many things needs to work together for the process described in the previous section to run smoothly. There are many decision points where trade-offs have been made between efficiency, generality, flexibility and available resources along the project.

Knowledge vs Content.

From the beginning of the project there have been divergences regarding the nature of the material developed for the project in OMDOC. From one viewpoint, it can be seen close to mathematical knowledge given OMDOC semantic nature. From another viewpoint, the semantic nature of OMDOC is moderated by the nature of the documents it encodes and the processing capabilities of the interpreters. Formal mathematical documents encoded in OMDOC should be written with consistency and completeness in mind. Their purpose is to represent knowledge that can be verified, proved and otherwise interpreted and used by computers. On the other hand, educational mathematical documents are written pedagogically, their purpose being to provoke learning experiences—which themselves are not usually represented explicitly in the document. Educational documents can be rather inconsistent, repetitive and incomplete, even on purpose if that is believed to improve their pedagogical effect.

The issue got acute when it came to decide the shape for the subject domain map in XLM. One possibility was to use the content available as a map, with content items (e.g. OMDOC concepts and symbols) being subjects of beliefs. On one hand, the approach is quick and simple, and it is the one used by LEACTIVEMATH old learner model. Authoring of new content would automatically update the map and every author could define topics for XLM to model learners on. On the other hand, it is an approach prone to inconsistencies, repetitions and incompleteness in learner models, very much as content could be. Another possibility was to develop an explicit ontological/conceptual map of the subject domain, as a more stable framework for XLM to ground beliefs on. Given the lack of a domain expert embedded in LEACTIVEMATH and able to interpret content and answer questions from it, a map of the domain would deliver part of the hidden, implicit content semantic. A map of the domain could help authors to better describe their content by making explicit references to the relevant parts of the map. On the other hand, since any subject domain can be described from many viewpoints, there can be many different, even conflicting maps of everything.

A third option was to use a collection of content dictionaries written in OPENMATH —the formal, XML-based mathematical language on which OMDOC is based. However, it was discarded because the content dictionaries were found inadequate, both in the topics covered and the relationships between them. A separate concept map for the subject domain was the implementation of choice for XLM, and so a hand-crafted domain map was implemented as part of XLM which covers a subset of Differential Calculus—the main subject domain of LEACTIVEMATH—and includes a mapping from content items to the relevant concepts, if available. It provides a solid ground for learner modelling which is less sensitive to changes in content.

Maps and Vocabularies.

The relationship between topics in the XLM domain map and content items is to some extent accidental. Nothing impedes content authors renaming their items nor map authors renaming their topics. A similar weak relation exists between the map for competencies used by XLM and the vocabularies used for specifying the relevant competencies in content metadata. They are based on the same framework and care has been taken for they to coincide, but this coincidence does not derive from a explicit link between them.

The mapping from content to topics is currently hardwired into the implementation of the domain map, hidden from content authors. In the same way, knowledge about vocabularies for metadata such as difficulty and competency level is hardwired into the code of XLM, particularly in event handlers and diagnosers such as the Situational Model and the Open Learner Model. There is no explicit link between this knowledge and the definition of the vocabularies.

Metadata Content and Usage.

A core but limited subset of the available content metadata is actually taken into account while interpreting events. Ignored metadata may describe important features of content that can be the reasons behind apparent contradictory evidence. Nonetheless, since most metadata for the current LEACTIVEMATH content has been produced based in the subjective appreciation of their authors rather than on empirical evaluation of content, it is suspected that there is a strong correlation between its different values. In such a case, taken into account more metadata elements can be misleading.

Propagation Algorithm.

A learner model in XLM is a large belief network constructed by composition of the maps that define the distinct dimensions of learners to be modelled. Every belief and evidence in this network is represented as a belief function . Propagators, that make use of the internal structure of the maps to propagate evidence, require the definition of a conditional belief function per association between elements in the maps. In the current implementation of XLM, however, a single conditional belief function is used for all associations in all maps, despite their many different types. A careful analysis of the maps and the propagation algorithm is necessary to determine suitable adjustments. On the same line, there are a few parameters that can be fine tuned to optimise XLM performance in terms of accuracy, reliability and efficiency. Of particular interest is the issue of performance with larger maps.

4 Towards a Generic Learner Modelling Engine

We have envisioned a future for XLM in which it can be easily embedded into other educational systems and even deployed as a learner modelling server. There have been a few attempts to do this in the history of research in intelligent tutoring systems (, , , ) with some level of success among the research community but no widespread usage outside of it. Besides the obvious moves of making XLM appealing by its core functionality as a learner modelling engine and improving its use of SemanticWeb technologies and standards, a proper parameterisation of its components would help XLM to better serve other educational systems. We can examine these issues from the perspective of the learner modelling process described in the section 2.

To start with, the number of maps used by XLM (figure 1), the way they are combined to set the framework for learner models (figure 3), the learner dimensions they describe and their internal structure need to be flexible. The maps should be encoded using a standardised language, such as XTM and supplied to XLM as parameters. An explicit and strong connection between the maps and vocabularies for metadata— depicted as greyed dotted arrows in figure 1—would be also beneficial.

Knowledge of the content, structure and semantic of event messages recognisable by XLM (figures 1 and 2) needs to be made explicit and accessible to users. It amounts to specifying a data model, as in SCORM , plus its intelligent processing. For example, the current implementation of XLM supports messages reporting log-ins and log-outs, starting and finishing exercises (including a measure of success rate), selfreports of affective states, diagnosis of motivational states and meta-cognitive skills, but all knowledge of how to interpret these reports is hardwired in the JAVA code of the event handlers.

Propagation of evidence in learner models would greatly benefit from specialised conditionals attached to the associations in the concept maps. Consequently, finding an easy way to do this becomes an important problem.We are exploring a possible solution to this problem by defining a conditional per type of association and adjusting it case by case, for each individual association on the maps, by taking into account the number of nodes each association connects—the more nodes connected, the conditional gets weaker.

For OLM, the visible facet of XLM, every event, map, metadata and vocabulary has to be provided with (internationalised) descriptions of their various constitutive elements, to be used in the graphical user interface to learner models. These descriptions are needed at various levels, as can be seen in figure 5.

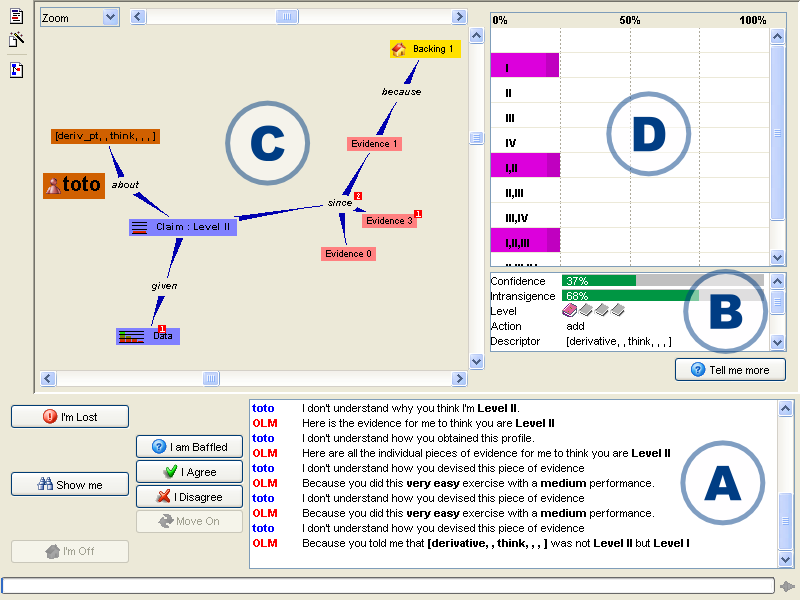
Fig. 5

A snapshot of the OLM Graphical User Interface.

Fig. 5

A snapshot of the OLM Graphical User Interface.

• Parameterising the evidence view (zone B of the interface, including a list of the important attributes of the event) means that important attributes have to be identified, their names and values to be described, as well as the (graphical) rendering used to display them in the list. For example, the attribute confidence in figure 5 is described as ‘confidence’ in an English context, its value defined as a percentage and rendered as a green progress bar.
• Parameterising the dialogue view (zone A, a verbalisation of the exchange between the learner and the OLM) means that a verbal description of OLM events have to be defined, including the templates to use and their arguments. For example, the challenge event presented in the interface shown in figure 5 is described by the template Because you told me that {0} was not {1} but {2}, using the belief descriptor, the previous summary level held by the XLM and the alternative statement made by the learner, respectively. The description of each argument needs to indicate how it should be formatted in the template.
• All references to belief elements need to be defined for their externalisation: descriptor, ability levels, and so on. For example, the belief descriptor (deriv_pt, _,think,_,_,_) needs to be transcribed according to the descriptions in the relevant topic maps (deriv_pt referring to the topic ‘derivative at a point’ in the domain map and think referring to the competency of ‘mathematical thinking’ in the competency map) and abstract ability levels currently used need to be mapped to the relevant vocabularies (for the case of a competency level, level II it could be transcribed as medium).

5 Conclusions

We have presented XLM, the learner modelling subsystem of LEACTIVEMATH, aWebbased educational system for mathematics. We have described XLM functionality, particularly in relation to its use of technologies related to the SemanticWeb, and discussed important design and implementation issues. Due to the fact that we aim at decoupling XLM from LEACTIVEMATH so that it can serve a variety of educational systems, we have discussed a minimum set of requirements to accomplish our goal, emphasising the need to parameterise XLM and improve its usage of Semantic Web standards and technologies. Striving to generality has been, together with open learner modelling, a salutory principle for XLM, yet the road ahead is full of challenges.

Acknowledgments

This publication was generated in the context of the LeActiveMath project, funded under the 6th Framework Programm of the European Community - (Contract N° IST- 2003-507826). The authors are solely responsible for its content, it does not represent the opinion of the European Community and the Community is not responsible for any use that might be made of data appearing therein.

References