A Contingency Analysis of LeActiveMath ’s Learner Model

Abstract

We analyse how a learner modelling engine that uses belief functions for evidence and belief representation, called xLM, reacts to different input information about the learner in terms of changes in the state of its beliefs and the decisions that it derives from them. The paper covers xLM induction of evidence with different strengths from the qualitative and quantitative properties of the input, the amount of indirect evidence derived from direct evidence, and differences in beliefs and decisions that result from interpreting different sequences of events simulating learners evolving in different directions. The results here presented substantiate our vision of xLM is a proof of existence for a generic and potentially comprehensive learner modelling subsystem that explicitly represents uncertainty, conflict and ignorance in beliefs. These are key properties of learner modelling engines in the bizarre world of open Web-based learning environments that rely on the content+metadata paradigm.

1 Introduction

What makes a good learner model? There are many answers to this question. From a pragmatic viewpoint, any representation of the learner that supports an educational system in providing better learning experiences to its users would qualify as a good learner model . From a more epistemological viewpoint, a good learner model must capture the significant aspects of a learner, predict her behaviour with accuracy and explain it convincingly . Consequently, learner models can be evaluated either by the benefits they bring to educational systems , the aspects of learners that they model , their predictive power or their explanatory power .

In this paper we explore the explanatory powers of XLM, a learner modelling engine developed in the LEACTIVEMATH project . XLM uses information on learner performance to maintain a collection of beliefs on different learner aspects such as their competencies, meta-cognitive skills, affective and motivational dispositions on a subject domain—Differential Calculus in the current implementation. XLM explanations of learner behaviour are the beliefs it holds on the actual levels (values) of these learner aspects, each belief supported by evidence constructed from interpretations of interaction events. We describe how XLM reacts to different configurations of input information about a learner in terms of changes in the interpretation of the input as evidence, changes in the states of its beliefs and the decisions that it infers from them. We compare XLM responses with our expectations as tutors and designers and make quality judgements. Our analysis is limited to XLM modelling of mathematical competencies on the subject domain. Specifically, we analyse:

a) the induction of direct evidence with different strengths depending on the qualitative and quantitative properties of the input (failing or succeeding on a very easy or very difficult exercise), b) the amount of indirect evidence derived from direct evidence, and c) the differences in beliefs and decisions that result from interpreting different sequences of events simulating learners evolving in different directions.

We finish the paper discussing outstanding issues, presenting our conclusions from the work so far and pointing to promising future work.

2 Learner Modelling Process and Belief Representation

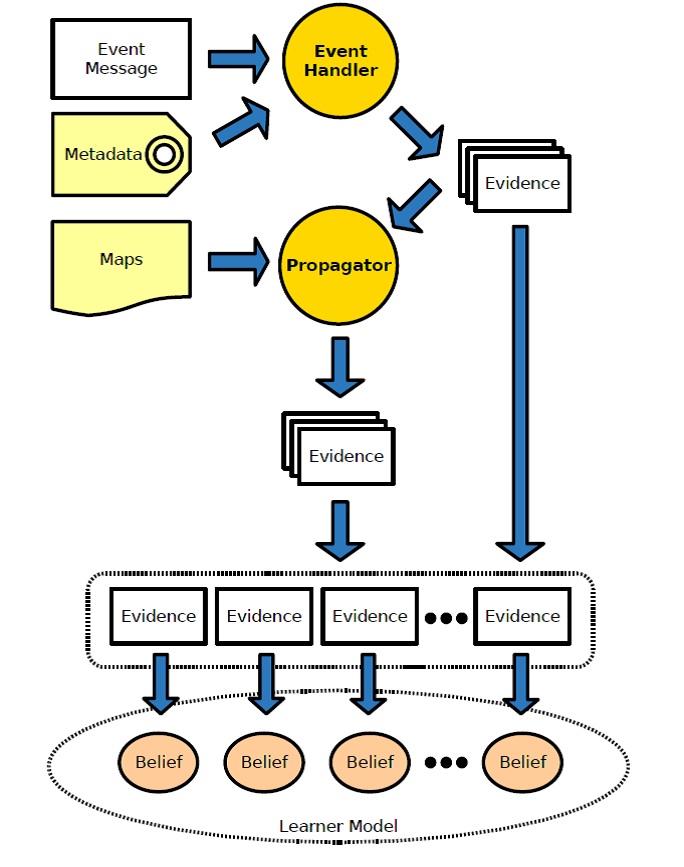
XLM is a learner modelling engine for a content+metadata type of system. It combines a simple issue-based approach , in which issues related to content items are identified in their metadata, with a generic multidimensional framework for learner models and belief functions as numeric knowledge representations . The mechanisms involved in the learning modelling process, from interpreting input information to deriving the corresponding evidence and finally updating beliefs based on it are sketched in figure 1.

Fig. 1

The learner modelling process.

Fig. 1

The learner modelling process.

A mass distribution is a belief function that can be interpreted as a generalised probability distribution whose domain is not the set of possible values of a variable but its power set—the set of sets of possible values of the variable. If we call $\Theta$ to the (finite) set of possible values of a variable, then a mass distribution is a function

In XLM, the variables are the learner aspects that it models—a variety of mathematical competencies, meta-cognitive skills and affective and motivational dispositions. Their values are levels in a scale of four,

and mass is distributed only among intervals, which are subsets of consecutive levels (i.e. subsets like ∅ and {I, II, III} but not like {I, II, IV}). Shorthands of the form X2Y are used in this paper to denote intervals (e.g. I2III is a shorthand for {I, II, III}) while a level name will be used to denote either a level or the set containing the level only, depending on the context. More details of XLM architecture, modelling framework, knowledge representation and modelling process can be found in .

3 Direct Evidence of Different Strength

The interpretation of reports of learner performance in exercises is based on the following assumptions:

a) the more difficult an exercise is, the more probable is to achieve a low performance, while the opposite holds for easier exercises, b) exercises designed for learners at higher competency levels are more difficult for learners at lower competency levels, and c) we can use a bell-shaped function, parameterised by an estimation of the difficulty of the exercise and the assumed competency level of the learner, to assign probabilities of performance.

Therefore, we assume that most learners would succeed on easier exercises, particularly on those aimed at competency levels lower than their own, and would fail on more difficult exercises, particularly on those aimed at higher competency levels than their own. Therefore, reports of these happening provide little information to update learner models and changes should be minimal. On the contrary, reports of failure on easier exercises and success on more difficult ones are more informative and should have a stronger impact on learner models.

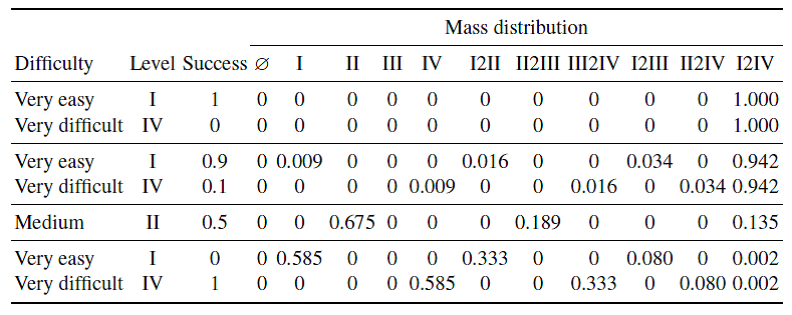
Table 1

Interpretation of prototypical reports of learner performance.

Table 1

Interpretation of prototypical reports of learner performance.

Table 1 shows the evidence induced from reports of the prototypical extremes of learner performance mentioned above, plus a couple of close approximations (nearly succeeding in a very easy exercise and nearly failing in a very difficult one) and an intermediate case of evidence induced from average performance on an exercise of medium difficulty designed for competency level II. The mass distributions in the first two rows, induced from the least surprising events, assign all mass to the set {I, II, III,IV}, which stands for the support the evidence gives to no level in particular, or total ignorance. These mass distributions can be interpreted as complete lack of evidence, representing in these cases the knowledge that “everyone succeeds on very easy exercises and fails on very difficult ones.” The next two rows contain the evidence induced from nearly succeeding (failing) in a very easy (difficult) exercise. In these cases, some mass have been taken away from ignorance (set {I, II, III,IV}) and distributed among other sets of levels. The third row, for example, indicates that nearly top performance in very easy exercises (success rate = 0.9) is interpreted as the learner being more probably at a competency level lower than level IV, yet XLM still leaves ample space to the possibility of the learner being actually at level IV. The process of moving mass away from ignorance reaches its limits in the case of the more informative events (the two rows at the bottom of the table) where the amount of (mass on) ignorance is minuscule in comparison to the mass assigned to the singletons {I} and {IV}, respectively, indicating that the events are interpreted as highly supportive of the learner being at a very specific competency level. Finally, for the case of the event of medium performance, the evidence induced is highly supportive of the learner being at the same competency level the exercise has been designed for, but still including its dose of uncertainty (mass on {II, III}) and ignorance.

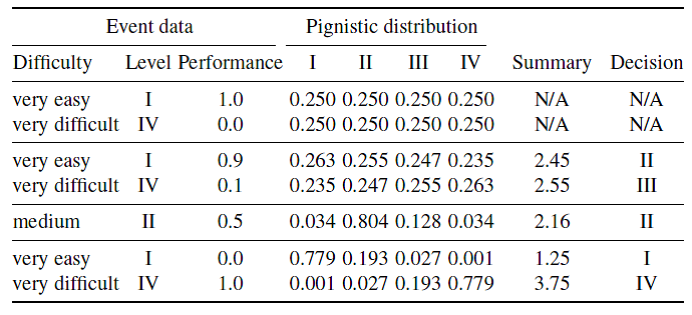
Table 2

Pignistic distributions, summary beliefs and final decisions on learner level from mass functions show in table 1.

Table 2

Pignistic distributions, summary beliefs and final decisions on learner level from mass functions show in table 1.

Table 2 contains details of information and decisions that can be inferred from the mass distributions shown in table 1. These are pignistic distributions, which are probability distributions derived from mass distributions , single value summaries and final decisions on the actual learner levels that would result from beliefs justified only by the single pieces of evidence in table 1. The table shows that XLM cannot make decisions under complete ignorance, yet it can be forced to make a decision in very close cases, as in the third and fourth rows in the table. These rows are interesting also because they show that currently XLM does not bet on the most probable level (level I and IV, respectively, in the pignistic distribution) but on the average. Decisions seem more straightforward in the last three cases which correspond to more informative event reports.

4 Amount of Indirect Evidence

Table 3

Amount of indirect evidence from single direct evidence.

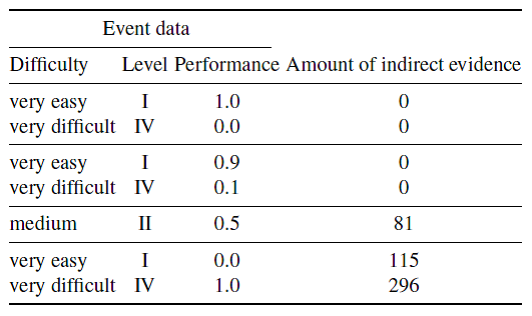
Table 3

Amount of indirect evidence from single direct evidence.

Table 3 shows how much indirect evidence is generated from the (direct) evidence induced from each one of the events discussed in the previous section. We expected the amount of indirect evidence to increase significantly from the events conveying less information to the events conveying more information, and the results shown in the table confirm our expectations. On the other hand, different amounts of indirect evidence are generated from the (equally) most informative events. An explanation of this happening is that the very difficult exercise is on derivative, the most connected topic in the domain map, hence predisposed to produce a large amount of indirect evidence even on the case of little information (but above the threshold defined in XLM). Finally, the amount of indirect evidence for the intermediate case falls in between the two extremes, as expected.

On average, the proportion of direct to indirect evidence in these cases is over 1 : 70. Assuming XLM can hold around 600 beliefs on mathematical competencies on the subject domain (around 30 domain topics and 20 competencies) this means that about nine exercises, evenly mapped onto the domain topics and competencies, would be required to have at least one piece of evidence (direct or indirect) per belief.

5 Beliefs and Sequences of Evidence

Reports of learner performance arrive as information becomes available as learners interact with content. A sequence of reports of learner performance reflects, in principle, the evolution of the learner as she interacts with the system and its content—learning, hopefully. XLM uses decay of evidence to account for the assumption that newer reports have more to do with the current state of the learner than old ones. Hence old evidence loses strength as new evidence accumulates—as if XLM were forgetting it.

In order to observe XLM responses to different sequences of events being reported we use three base sequences: one standing for improvement, another one standing for deterioration, and yet another one standing for random performance. Each sequence consists of seven events, each one reporting the success rate of the learner on an exercise of medium difficulty at competency level II. In addition, we used two more sequences derived from the improvement and deterioration sequences by introducing random variations in the range [−0.1,0.1](figure 2).

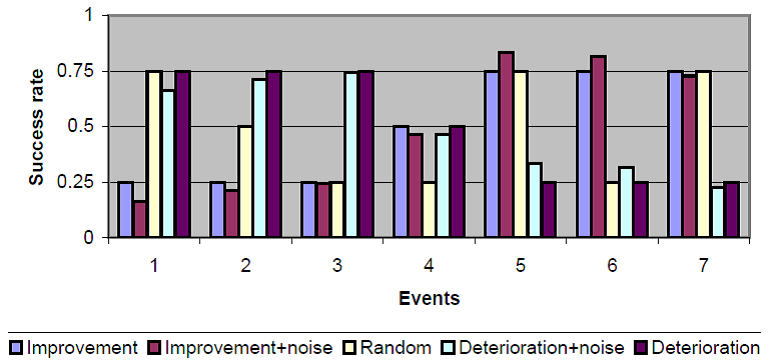
Fig. 2

Sequences of performance used to assess XLMresponses to the order in which information arrives.

Fig. 2

Sequences of performance used to assess XLMresponses to the order in which information arrives.

XLM responses to these sequences are shown in figures 3 and 4, and table 4. The figures include graphs illustrating the evolution of beliefs on the mathematical competency of the learner regarding a domain topic addressed by the exercise, using summary beliefs (figure 3) and pignistic distributions (figure 4) to make changes in the beliefs easier to visualise. Table 4 contains the full mass distribution for the final belief resulted from each sequence of events.

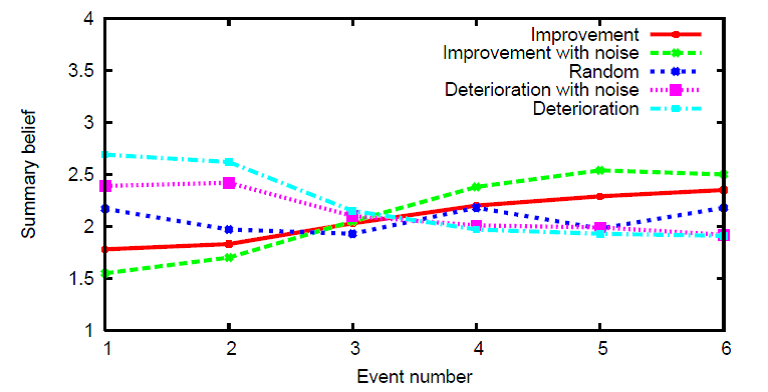
Fig. 3

Evolution of summary belief for all sequences.

Fig. 3

Evolution of summary belief for all sequences.

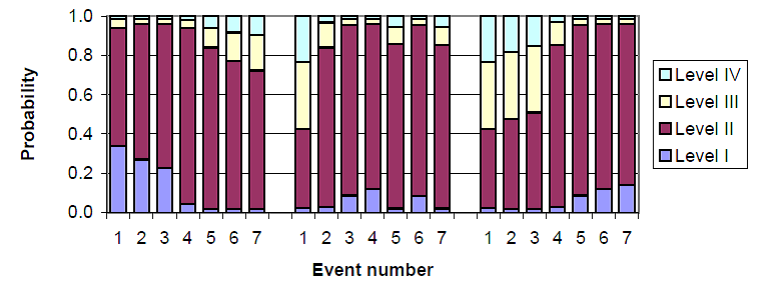
Fig. 4

Evolution of the pignistic distribution along the improvement, random and deterioration sequences, displayed in that order from left to right.

Fig. 4

Evolution of the pignistic distribution along the improvement, random and deterioration sequences, displayed in that order from left to right.

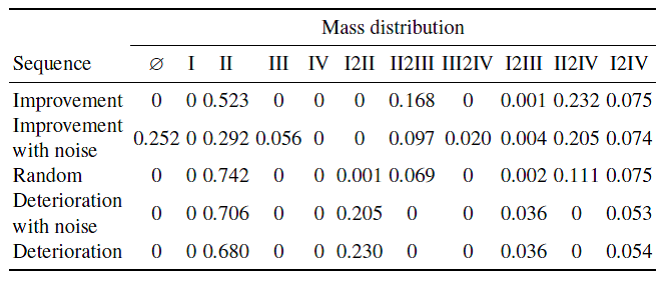
Table 4

Final beliefs for all the sequences of events.

Table 4

Final beliefs for all the sequences of events.

It can be seen that XLM reaction to the sequence of evidence standing for improvement is a belief that evolves steadily from something like ‘level II, or perhaps lower’ to something more like ‘most certainly level II, yet may be higher’ as more evidence accumulate, while still conceding a very small amount of possibility to the case of the learner being at competency level I. The belief derived from the sequence of evidence standing for deterioration evolves from something like ‘II or over’ (actually, the summary belief is very close to level III while a hint of possibility is given to the learner being at level I) to something like ‘level II, but could be lower.’ The belief for the random sequence evolves somehow “in between” the beliefs produced for improvement and deterioration, strongly favouring level II as expected, given the fact that the exercise is of medium difficulty for competency level II.

The beliefs that result from considering the noisy sequences follow in general the patterns of the corresponding base sequences. Due to the nature of the noise introduced (random noise that happens to be more negative than positive, specially for the first half of events) it accentuates the improvement effect and attenuates the deterioration one, so that the final belief in the former case considers level III as a strong alternative to level II (mass in sets {III} and {III,IV}) while in the latter case the support for level II increases (slightly more mass on {II}) as the support for level I decreases (less mass on {I, II}).

Finally, the belief resulting from the sequence of improvement with noise (second row in table 4) assigns one quarter of the mass to the empty set, indicating in this way that the belief is based on divergent evidence, corresponding in this case to steep improvement.

6 Discussion

The current interpretation of reports of learner performance by XLM is based on its designers’ common sense and some basic mathematical techniques (e.g. bell-shaped probability assignments resembling normal probability distributions). The evidence and beliefs that result from the interpretation of the reports look reasonable and mostly intuitive. They also illustrate how uncertainty and ignorance are represented in belief functions differently from how they are represented using probability distributions.

A few issues are worth mentioning here. The most important one is perhaps the lack of theoretical or empirical support to the current interpretation of events, despite how reasonable it may seem. Although we can justify our approach on the basis of the great amount of subjectivity in metadata—not necessarily a peculiarity of LEACTIVEMATH content—a sounder design of the interpretation process based on some psychometric theories would have its advantages. Another important issue concerns the use of a learner model in the interpretation of relevant events, which has been avoided in this paper. Actually, XLM includes two modes for incorporating new evidence into existing beliefs: an objective mode, in which the strength of new evidence is independent of the existing beliefs, and a biased mode, in which new evidence is considered on the light of the existing beliefs—e.g. ‘It is hard to believe that such a good student had such a bad performance by any other reason than by accident.’ However, the experiments described in this paper use the objective mode only.

Once all relevant information concerning an event is made available by LEACTIVEMATH, the first step in its interpretation by XLM consists in deriving a probability distribution from which a mass distribution standing for the evidence is generated . Quite probably this step, which includes both the construction of the probability distribution and the specific algorithm used for its translation into a mass distribution, is unnecessary and may have a limiting effect on our use of belief functions as core knowledge representation formalism. Furthermore, the fact that we have resorted to summary beliefs and pignistic (probability) distributions to describe a core part of XLM behaviour, how beliefs change along time, is a consequence of the difficulties to visualise, apprehend, meaningfully manipulate and produce clear external representations of belief functions. These difficulties have been markedly evident in our efforts to construct open learner modelling functionality in XLM.

7 Conclusions

In this paper we have presented an analysis of how a new learner modelling engine we call XLM reacts to changes in the characteristics of its input information. Despite the fact that our analysis is modest in its coverage of the space of possible input data—in particular, it does not include the interpretation of input information concerning metacognitive skills nor motivational and affective dispositions—it is suggestive of XLM responding appropriately to available information regarding learner behaviour.

Further work on the line presented in this paper includes extensive analysis of XLM response to learner behaviour. For example, the effect on learner models of evidence propagation as learners course through educational content, differences in learner models that result from updating beliefs using either the objective or the biased mode, the interpretation of learner actions on an open learner model as evidence for meta-cognitive skills and the interpretation of learner behaviour for modelling motivational and affective dispositions. We plan also to carry out sensitivity analyses of the collection of explicit and implicit parameters that control a great deal of XLM behaviour.

We interpret the results presented in this paper as substantiations of our vision of XLM is a proof of existence for its kind: a generic and potentially comprehensive learner modelling subsystem that uses belief functions for encoding its beliefs because they facilitate the explicit representation of uncertainty, conflict and ignorance. These are key properties of learner modelling engines in the bizarre world of openWeb-based learning environments that rely on the content+metadata paradigm.

Acknowledgments

This publication was generated in the context of the LeActiveMath project, funded under the 6th Framework Programm of the European Community - (Contract N° IST- 2003-507826). The authors are solely responsible for its content, it does not represent the opinion of the European Community and the Community is not responsible for any use that might be made of data appearing therein.

References

Notes