Representational Decisions When Learning Population Dynamics with an Instructional Simulation

Abstract

DEMIST is a multi-representational simulation environment that supports understanding of the representations and concepts of population dynamics. We report on a study with 18 subjects with little prior knowledge that explored if DEMIST could support their learning and asked what decisions learners would make about how to use the many representations that DEMIST provides. Analysis revealed that using DEMIST for one hour significantly improved learners ’ understanding of population dynamics though their knowledge of the relation between representations remained weak. It showed that learners used many of DEMIST’s features. For example, they investigated the majority of the representational space, used dynalinking to explore the relation between representations and had preferences for representations with different computational properties. It also revealed that decisions made by designers impacted upon what is intended to be a free discovery environment.

1 Introduction

Research with multi-representational tutoring systems and learning environments has revealed that learning with multiple external representations is a demanding process but one that if successfully mastered can lead to a deep understanding of the domain, e.g. . DEMIST is a multi-representational simulation designed to explore when learning with MERs is effective. It implements the DeFT framework for learning with MERS and by evaluating how people learn with DEMIST, we also evaluate the underlying framework. This serves a dual function. By analyzing learners’ behaviour we can understand more about the demands of complex information processing and by understanding these demands adaptive multi-representational learning environments can be created. To accomplish this, we intend to perform design experiments based on manipulating the parameters of the DeFT framework. However, before this can be achieved we have sought to discover if DEMIST is effective and how learners would respond to an environment which provides so much representational flexibility. To begin we therefore summarise the DeFT framework and how DEMIST embodies it before turning to the details of the study.

The DeFT Framework provides an account of the different pedagogical functions that MERs can play, the design parameters that are unique to learning with MERs and the cognitive tasks that must be undertaken by a learner.

There are three key functions of MERs: to complement, constrain and construct. MERs complement each other by supporting different complementary processes or containing complementary information. When two representations constrain each other, they do so because one supports interpretation of the other. Finally, MERs can support the construction of deeper understanding when learners abstract over representations to identify the shared invariant features of a domain. Each of these functions has a number of subclasses (see ). The cognitive tasks that a learner must perform to learn with MERs include understanding the properties of the representation and the relation between the representations and the domain. Additionally, learners may have to select or construct representations. The cognitive demand unique to MERs is to understand how to translate between two representations and there is much evidence that this is complicated. DeFT describes five key design dimensions that uniquely apply to multi-representational systems:

1. Redundancy: How information is distributed. This influences the complexity of a representation and the redundancy of information across the system;
2. Form: The computational properties of a representational system;
3. Translation: The degree of support provided for mapping between representations
4. Sequence: The order in which representations are presented;
5. Number: The number of (co-present) representations supported by the system.

DEMIST allows systematic manipulations of these design parameters. It aims to support learners in the development of their knowledge of the concepts and representations important in understanding population dynamics. It provides a number of mathematical models, for example, the Lotka-Volterra model of predation which learners can explore. To investigate these models, users are presented with a potentially very large set of representations. Hence, DEMIST also aims to support learners” understanding of how domain general representations such as X-Time graphs are used in this domain, to introduce them to the specific representations of population dynamics (such as phaseplots and life tables) and to encourage their understanding of the relationship between these representations.

The study we report in this paper represents the first attempt to evaluate if DEMIST is effective. However, an equally important goal was to discover how learners would use a simulation-based learning environment which includes so many representations. We subscribe to the view that learning is best considered an active process where learners take responsibility for their own achievements, but were worried about whether DEMIST provides sufficient support to guide learners new to the domain. Therefore a key design goal was to keep track of users’ behaviour with DEMIST. Furthermore, few simulation environments provide learners with quite so much choice about what representations to interact with and how many to work with simultaneously. Therefore we have little information about learners’ representational preferences. Hence, this experiment explores decisions learners make when provided with many complex representations.

2 System Description

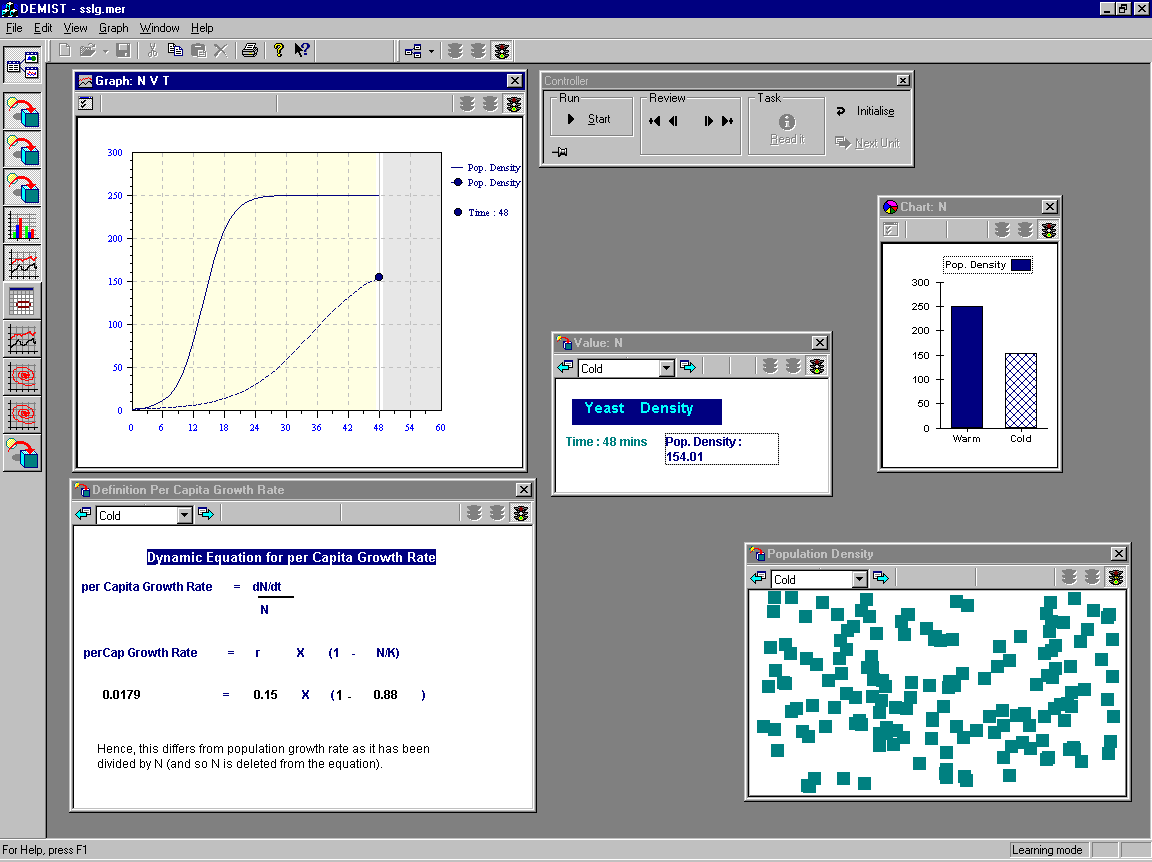
DEMIST (see figure 1) is built around the authoring of instructional scenarios. The basis for its design is a formal description of an instructional simulation that describes the task of authoring simulations with SIMQUEST . Each scenario consists of a sequence of Learning Units that instantiate a particular mathematical model. The parameters of the mathematical model are combined as experimental sets that can be instantiated by various sets of initial conditions. This allows the learner to explore the same model under different experimental conditions.

Figure 1

DEMIST in learning mode.

Figure 1

DEMIST in learning mode.

Each of these Learning Units includes a set of representations such as table, XYGraph, Histogram, Animations which display one or many of the variables and parameters extracted from the mathematical model. Representations can be automatically displayed or only shown when the learner requests them and the order in which they appear can be specified by an author or left under learner control. One of the features of DEMIST, unique to our knowledge among the simulation environments, is that the translation between representations can be varied. DEMIST currently allows three levels of translation: independent (actions on an ER are not reflected onto other ERs), map relation (selecting a value in one ER shows all the corresponding relationships in other ERs) and dyna-linked (modifying the information in one ER is reflected onto all the other relevant ERs). There are a small number of additional activities available to the learners. In particular, they can make hypotheses about the values of the model in the future or perform actions, which allows the learner to act on a value at the current stage of the simulation and change it. They can choose which representations they use to perform these activities and depending on the degree of translation could check the consequences of these actions on other representations (e.g. predict that the population density will have doubled in size in 10 years by adding a hypothesis to the relevant row of a table and see a point added to the graph corresponding to that prediction).

3 Method

The experiment used three of DEMIST’s models of population dynamics, starting from the simplest: Single-Species Unlimited Growth (SSUG), Single-Species Limited Growth (SSLG) and Two-Species Predation (TSP). Each of these models consisted of three learning units, which focused on particular phenomena that is characteristic of that model (e.g. doubling time for exponential growth, carrying capacity for limited growth ). The learning units specified the representations to be included and any learning activities to be performed. To provide learners with a large relatively unconstrained space to explore, the following authoring decisions were made:

• Information: representations contain up to three dimensions of information. Pairs of representations could therefore have full, partial or no redundancy;
• Form: large representational system (between 8 to 10 ERs for each unit), which varied in their relevance and ease of interpretation;
• Sequence: learner choice of sequence of representations;
• Number: a maximum of five co-present representations. A small number of representations were selected to be displayed at the beginning of each unit;
• Translation: full dyna-linking allowing learners to reflect actions onto other ERs.

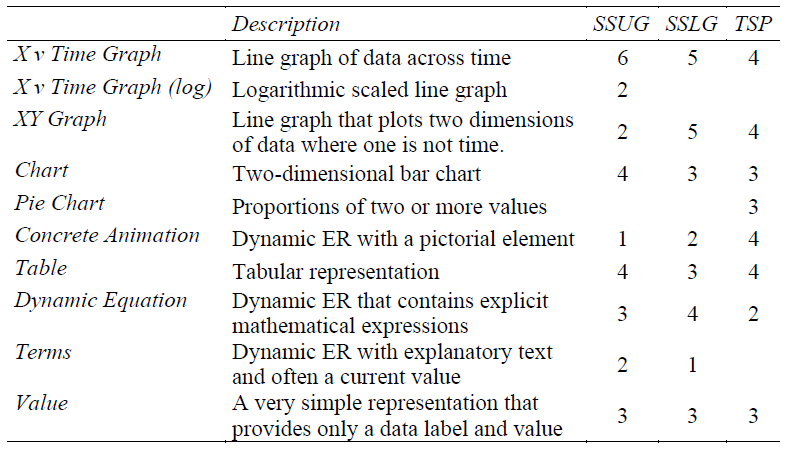
For the purposes of this study we were less interested in examining the informational properties of a representation. Hence, we categorised the representations according to a taxonomy of representation type which focused on the format and operators of the representations. For example, all tables were classified as one type of representation, tabular, whether they contained values of population density, growth rate or environmental resistance. Similarly all representations that could have been considered as animations were so grouped. The analysis of the type of representations provided in the experiment together with the number of representation of each type available by model can be seen in table 1.

Table 1

Categorization of ERS in DEMIST.

Table 1

Categorization of ERS in DEMIST.

3.1 Participants

18 participants were involved in the experiment. All were students or researchers at Nottingham, and their prior experience in mathematics and biology was recorded (students with degrees in biology or mathematics were excluded from the experiment). One of them crashed the software during the experiment, making the data unreliable for analysis. The results are based on the remaining 17 participants.

3.2 Pre and Post-Test

The pre-test and the post-test consisted of multiple-choice questions, 11 for the former, and 22 for the latter. The pre-test was developed to assess whether subjects had any relevant prior knowledge and was deliberately designed to include items that were most likely to be familiar. The post-test included more difficult items and repeated 10 of these pre-test questions. One key feature of the questionnaire design was the development of three types of question. The first focused on domain concepts (e.g. what will happen to the prey population if some predators are removed?), the second on interpreting specific representations (e.g. which of these four graphs of population density against time is characteristic of SSUL?) and the third on multirepresentational understanding (e.g. finding the odd-one-out among four different representations of supposedly the same dataset). These questions were designed to assess if multi-representational simulations such as DEMIST can support learning about representations and the relation between representations as well as the more traditional conceptual issues.

3.3 Procedure

Participants were first given the un-timed pre-test and were then introduced to DEMIST and the main features of the interface explained. The experimenter remained present to clarify any questions that learners may have about the interface but did not provide direct guidance. Participants were warned they only had one hour to complete the three tasks and the experimenter occasionally reminded them about the time. However, generally participants had complete control over the amount of time and the nature of their interactions with DEMIST. After one hour, participants were stopped and immediately given the post-test. They completed the test in their own time and were then debriefed and paid for their participation.

4 Results

The learners had some prior knowledge of the domain. If they had been guessing, they would have been expected to get a total of 25% of the questions right as each question had one right answer and three distractors. As can be seen from table 2, the average pre-test score was 42.3% which is significantly above chance (t= 4.3, df = 16, p < 0.001).

Table 2

Pre-Test and Post-Test results.

Table 2

Pre-Test and Post-Test results.

Closer analysis revealed whether or not questions of different types (i.e. conceptual, single ER, MERs) were answered differently. Conceptual and Single ER questions were answered above chance, however those relating to MERs were answered significantly below chance (t = 2.5, df= 16, p=.024). This pattern of results confirms our intuitions that these types of question were harder than the others.

The post-test consisted of 10 items from the pre-test and 12 more items. Again the performance of participants was significantly above chance at 55.6%, (t= 8.5, df = 16, p<.0001). Table 2 shows that overall there was a significant increase in the percentage of questions that subjects got right from pre-test to post-test (t = 3.1, df =16, p<0.008). As the post-test included more difficult items than the pre-test, we compared subjects’ performance on those questions that were present on both the pre and post-test. Scores significantly improved on these questions from an average of 45.9% at pre-test to 62.3% at post-test (t = 4.9, df = 16, p <.0001). Finally, we looked at performance on post-test items by type of question. Performance on all questions was now significantly above chance accept for those questions which dealt specifically with MERs (t=1.4 df = 16, p=.188) which was now at chance.

There was only limited time available for this intervention and in future we would like to have longer sessions. So given these factors we are content to observe significant improvement in learning outcomes.

4.1 How Do Learners use DEMIST?

The second goal of the study was to explore learners’ representation use to discover whether they had strong preferences about the representations.

Number of Simultaneous Representations

Learners had the choice to work simultaneously with between one and five representations plus the controller. The majority of learners spent most of their time working with three representations (40.4% of total time) or four representations (31.7%). Working with one representation at a time was very unpopular and working with two only slightly more common. There is a relatively high standard deviation for the use of 5 co-present representations (mean 19.1%, St.Dev. 13.12%). No one chose to use the maximum number of five representations for more than half the session and some participants never used more than four representations.

Exploration of the Representational Space

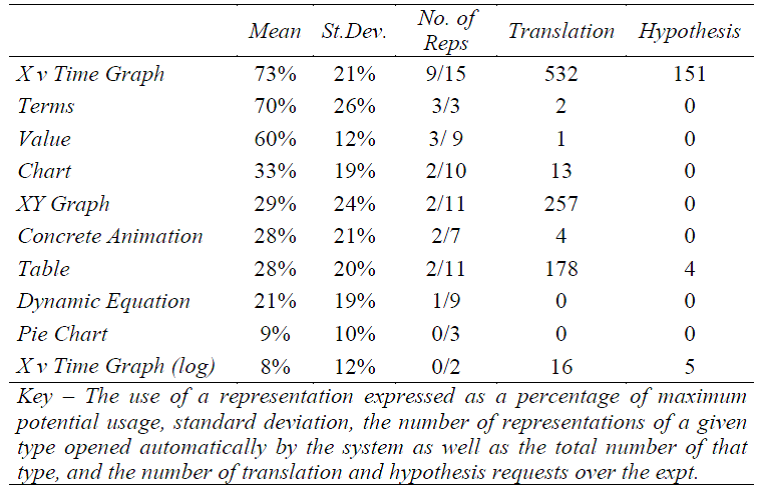
We examined the total number of representations that the participants activated (using a time threshold of 10 seconds to avoid including Ers opened in error). Participants tended to explore as much as possible of the representational space, activating a total of 73 representations on average out of the 80 available. However, this does imply that they used the representations equally. To examine which representations learners preferred we calculated the amount of time each type of representation was used. As not all representations were available in all learning units, we first calculated the maximum possible availability (see table 1). Secondly, we grouped all representations of the same type together even if they contained different information. This allowed us to express the use of each type of representation as a function of its availability. So, for example in table 3, the low value for the pie chart does not mean that it was available rarely, it shows that even when available, it was not selected.

Table 3

External Representations Usage.

Table 3

External Representations Usage.

The first analysis we performed on this data was to examine how influenced learners had been by the initial selection of representations for a unit. During piloting it had become evident that some learners were unhappy unless they were provided with an initial set of representations, hence for each unit we selected two or three representations to open automatically. However, learners were free to close those representations at any time. We found a striking correlation between our provision of representations and the ones that learners spent the most time working with (r = 0.85, n = 10, p < 0.02). For this reason, a large degree in the variance of percentage of use is not based on a learner’s choice of representations, it is based on the system’s choice. The ERs that learners selected for different amounts of time than that predicted simply by automatic selection include the XY graph which was used more than expected, and the table and concrete animation, which were used less.

Acting on Representations

Representations are used for both display and action, where actions are a request to translate information, predict a value at some future point or to modify current values. The trace logs provided information about which ER was associated with the initiating action for translating and for stating hypotheses. The total number of these requests for the 17 participants can be seen in table 3. There is enormous variance in these values. The X v Time Graph was used for 98% of all hypotheses. For translation requests, again the X v Time Graph was the most common accounting for 58% of all requests, but the XY Graph (25%) and the Table (12%) were also used appreciably. These latter figures are particularly interesting as they do not reflect the percentage of time that learners chose to display the representations (see table 3). Translation requests from the XY graph are plausibly about trying to understand a new and difficult to interpret representation, whereas from the table perhaps its familiarity was being used by learners to help interpret other representations.

5 Discussion

This study provides useful information to begin work on design experiments on the DeFT parameters. They have confirmed that DEMIST can teach learners with little prior knowledge about the representations and concepts involved in population dynamics. This is encouraging as in normal use we would expect to allow learners to use DEMIST for substantially more than the one hour available for this study.

Analysis of the test material has shown that understanding the relation between representations may be the most difficult aspect of the domain. Learners performed worse on these items at pre-test and only got 34% of the MERs answers right at posttest. This confirms earlier studies which have shown that relational understanding is difficult for learners (e.g. ). How best to support translation between representations, is one of the aspects of DeFT that has been implemented in DEMIST. We can vary the level of automatic support between ERs in ways that we refer to as contingent translation. Learners new to the domain should be provided with fully dyna-linked MERs. This scaffolding will be reduced as their knowledge improves so that they take increasing responsibility for mapping information across ERs. The relatively poor performance on the MERs items in the study provides further evidence for the importance of empirical research in this area and highlights the need to develop test material that is sensitive to multi-representational understanding.

This study was also concerned with addressing how learners would behave if they were given the representational flexibility that DEMIST provides. We were interested in exploring what their representational preferences were and whether they would spontaneously choose to use features such as translation. A number of interesting details were revealed about learners’ behaviour, some of which we had no t expected.

Firstly, we were disconcerted to observe how much of learners’ representational selection was based on an initial set of representations presented by the computer. Essentially, the vast majority of learners chose to work with these representations only exploring alternatives towards the end of a learning unit. This may well cause us to redesign the learning units. The decision to “pop up” pre-selected representations had been made after piloting. However, we viewed the system presentation of representations as gentle guidance about useful places to start and emphasised this during the introduction to the system. This does not seem to have been learners’ interpretation. Of course, perhaps we chose the “best” representations for each unit and the learners simply agreed with this choice. This is possible as we based our selection of representations on the way that they were used in textbooks (e.g. ). A future experiment could compare different ways of selecting initial ERs varying between none/random /“worst”/“best” to provide information about how much guidance a supposedly discovery environment like DEMIST ought to provide.

Other results that may have implications beyond DEMIST’s domain include the number of co-present ERs that learners chose to use. There was a strong bias for three or four ERs. Learners rarely chose to focus on only one or two at a time. Some learners did seem happy to go to five, the maximum we allowed in this study but others limited their selection to three. Many simulation environments provide a fixed number of representations. We would argue that ideally this decision should be under learner control, but where not, limiting the number of co-present ERs to three or four seems to fit with most learners representational preferences.

We also examined learners’ actions to see which ERs were used to request translations. Learners made quite a number of translation requests (an average of 59 per participant). The majority of these were from the X-Time graph but significant numbers were from the XY graph. This was surprisingly high given its low general percentage presence. We interpret this behaviour of one of attempting to use DEMIST’s translation features to understand this complex representation by relating it to other more familiar representations. We had expected to see more learners selecting familiar representations and requesting translation from this known point. This was arguably what occurred with the table. However, representations such as “value” which we had included for this function were not used in this way. It provokes an interesting instructional question of whether learners should start from the familiar and interpret a new representation from its standpoint or start with the unfamiliar and complex and then see how it relates to the familiar. Finally, learners only stated hypotheses with X-Time graph. This is disappointing as one of the benefits of dyna-linking is that learners could construct hypotheses on different ERs and see how this was mapped to other ERs. For example, they could have added values to the table (which is an easy and precise operation) and then this value would be reflected onto other representations such as the XY graph. We need to find a way to emphasise this strategy as it is a more active way of understanding relations between representations than simply selecting common dimensions of information.

We had expected to observe a systematic relationship between representation usage and learning. There was no evidence for this. One reason for this may be the lack of variability between learners’ ER use – e.g. sticking to system selection, examining but not really using all of the representation space, choosing three or four representations, etc. However, this result also highlights a flaw in relying solely on the traditional experimental method. For example, if learners chose to spend a large amount of time with an XY graph, we can’t tell from the traces if the explanation is that they didn’t understand the representation and were trying to interpret it or whether they were in fact fully conversant with it and recognised that it was a useful way to understand the domain. If we want to understand the process of learning with MERs we need to take a more fine-grained approach to data collection. A key next stage in the project will be to conduct a micro-genetic study (e.g. ) with one or two learners where we will take detailed protocols about their goals, strategies and decisions.

This study has revealed DEMIST to be a suitable environment to ask questions about how learners should best be supported when they learn with MERs. It is based on a rich domain which is best understood by reference to multiple linked representations. We have shown that students can begin to understand the domain in a short amount of time but that the more complex issues will require more time and strategic support. Hence, we will be following a two-pronged research agenda. Using detailed protocol analysis we hope to build a more complete picture of the process of learning in this domain which could ultimately form the basis of a computational model (e.g. ). Second, we can perform design experiments which systematically vary the DeFT parameters (e.g. amount of translation, number of co-present ERs). A combination of these two approaches should help uncover design principles for how best to support the complex information processing that MERs require.

References