Applying the DeFT Framework to the Design of Multi-Representational Instructional Simulations

Abstract

Learning environments use multiple external representations (MERs) in the hope that learners can benefit from the properties of each representation and ultimately achieve a deeper understanding of the subject being taught. Research on whether MERs do confer these additional advantages has shown that learning can be facilitated but only if learners can manage the complex tasks associated with their use. Our approach examines how the design of learning environments influences the cognitive task demands required of the learner with the longer term goal of using these findings to develop more adaptive and supportive multi-representational environments. In this paper, we begin by summarising the key features of the DeFT framework and then illustrate how such a framework can be used to classify existing systems. The main body of the paper describes the architecture of an instructional simulation that embodies DeFT. Finally, we conclude by illustrating the research questions we hope that experiments with this system can answer.

1. Introduction

Many advantages are claimed for multi-representational learning environments. By using multiple external representations (MERs), it is hoped that learners can benefit from the properties of each representation and that ultimately this will lead to a deeper understanding of the subject being taught. Consequently, many systems provide (or allow users to construct) MERs of the domain. Typical systems include HYPERPROOF , which teaches analytical reasoning and proof construction, using a diagrammatic blocks world and sentential, predicate logic. By providing the graphical representation, students can focus on the information content of proofs rather than the syntactic structure of sentences. SWITCHER is a multi-representational construction environment. Students answer constraint satisfaction problems by building (and switching between) representations such as diagrams, tables, textual and logical representations. STATPLAY is designed to help eradiate misconceptions about statistics especially in the areas of sampling variability and conditional probability. It uses multiple (linked) representations such as the curve and the statistical values of a distribution. As a learner alters values of the mean and standard deviation, the graph of the distribution changes in accordance with these values.

However, research that has evaluated how effectively multi-representational environments support learning has produced mixed results. Many studies have found benefits for MERs. For example, learners who solved algebra word problems with MERs were about twice as effective as those who used just one representation . Even young children can learn effectively with MERs if they are given appropriate combinations of representation . Children were taught to provide multiple solutions to mathematical coin problems. Those given a tabular representation of their answers, in addition to the canonical place-value representation, produced significantly more solutions on a post-test than those who interacted with just the place-value representation.

Conversely, many studies have shown that learners find working with more than one representation to be very difficult. For example, learners were provided with qualitative representations to help them solve inductive physic problems. But, there was no evidence that they used this knowledge to reduce the search space of equations considered . Furthermore, combining pictures with mathematical expressions can be less effective than (informationally equivalent) representational systems that are both mathematical or both pictorial . Yet, this particular combination is so often favoured in multi-media systems.

Examining these apparently contradictory findings, it is apparent that the learning environments were used for diverse pedagogical goals, included numerous forms of representational system and were designed in many different ways. Unsurprisingly, generalisations concerning the effectiveness of multi-representational environments are difficult to achieve. Nonetheless, these findings demonstrate that MERs do confer additional advantages if learners manage the complex tasks associated with their use.

We propose that the field of Artificial Intelligence in Education can contribute to the design of effective multi-representational learning environments in two ways. First, by taking a cognitive science approach, we can help uncover how the design of the environments influences the cognitive task demands required of the learner. Second, by understanding these demands, more adaptive and supportive multi-representational learning environments can be created. In this paper, we will describe one such approach to this research agenda – the DeFT Framework. We begin by summarising its key features, then describe how it has been embedded in an instructional simulation (IS) and conclude by illustrating the type of research questions we hope it can answer.

2. The DeFT framework

The DeFT (Design, Functions, Tasks) framework for multi-representational learning environments sets out a number of important questions that designers and teachers should ask in order to provide effective learning experiences for their students. It provides an account of the different pedagogical functions that multiple representations can play, the design parameters that are unique to learning with more than one representation and the cognitive tasks that must be undertaken by a learner when interacting with MERs.

There are three key functions of multiple representations: to complement, constrain and construct. When MERs complement each other they do so because they support different complementary processes or because they contain complementary information. When two representations constrain each other, they do so because one supports possible (mis) interpretations of the other. For example, a familiar representation can help a learner come to understand a less familiar representation. Finally, MERs can support the construction of deeper understanding when learners abstract over representations to identify what are shared invariant features of a domain and what properties of individual representations. Each of these functions has a number of subclasses (see for further details).

Tasks refer to the common cognitive tasks that a learner must perform in order to successfully learn with MERs. These will differ depending upon a learner’s familiarity with the representation and the domain, and the use to which representations are put. For example, when presented with representations, learners must understand the properties of the representation and the relation between the representations and the domain. Additionally, they may have to select suitable representations, construct known representations or develop new representations for familiar or unfamiliar problems. The cognitive task unique to learning with MERs is to understand how to translate between two representations and there is abundant evidence that this can be very complicated.

In common with all learning environments, design decisions such as teaching strategies, nature of help provision, domain content, etc. must be considered. In addition, there is a set of design dimensions that uniquely apply to multi-representational systems and it is these that are considered here. Five key parameters are considered in the framework at present:

1. Redundancy: In multi-representational environments, designers can chose how information is distributed over representations. This influences the complexity of each representation and the redundancy of information across the representational system;
2. Form: The computational properties of the representational system (e.g. does it combine text and graphics);
3. Translation: The degree of support provided for mapping between two representations. This can range from no support through to highlighting and on to full dyna-linking where behaviour on one representation is reflected onto another;
4. Sequence: Many systems present only a subset of their representations at one time, consequently two further decisions must be made - in what order to present the representations and when to change the representations that are displayed.
5. Number: The number of representations supported by the system.

One use of this framework is to examine the design and functions of existing systems. For example, MERs are commonly used in instructional simulations . Most of these environments exploit the abilities of MERs to constrain interpretation of an unfamiliar representation by providing a concrete representation (e.g. the rocket skater with the velocity-time graph in DM3 ) Another regularly observed function is the use of MERs to provide different computational properties (e.g. REMISS-CL , which reveals alternative aspects of elastic collisions by using one-dimensional property diagrams and velocity-velocity graphs). There is less explicit mention of the use of MERs to encourage deeper understanding, although this may be implicit in the designers’ goals. There is even more diversity in how these systems are designed. Taking a single design feature such as automatic translation we can see that some systems provide full dyna-linking between representations (e.g. MODELLUS ), whereas others provide no support at all for learners (e.g. CENTS ). It is this diversity in design and the resulting lack of agreement about appropriate ways to support the different functions of MERs that DeFT is intended to address. Consequently, we created a dedicated Multi-Representational Instructional Simulation (MRIS) environment, called DEMIST (Design Environment for Multi-representational Instructional Simulation Technology) that allows systematic manipulations of design parameters. Its architecture is described in the following section.

3. An architecture for a MRIS environment

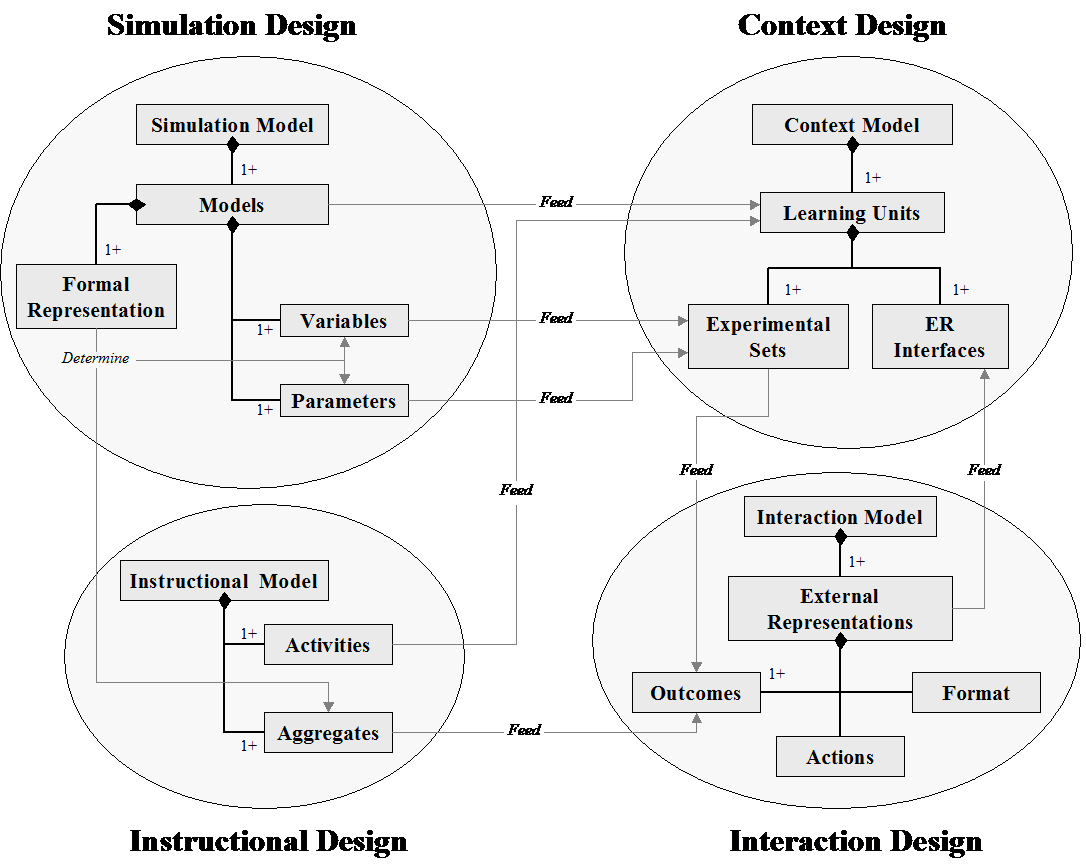
Many general-purpose simulation environments and authoring tools exist (e.g. MODELLUS , STELLA , SIMQUEST ). However, these environments are primarily concerned with flexibility of modelling and simulation, whereas we emphasise representational flexibility. The basis for the design of DEMIST is a formal description of an IS that describes the task of authoring instructional simulations with the environment SIMQUEST. This was adapted to our needs and then we applied DeFT to the representational issues.

As is SIMQUEST, our environment is based on a four-part model (Figure 1), each of them provided with its own design procedures. These models, their role, their characteristics, the relations that link them, and the internal elements that need to be specified in order to build an instructional simulation scenario, will be described in the following section, organised as a heuristic device, by Palmer’s analysis :

• The represented world, which introduces the Simulation Model;
• The representing world, which introduces the Interaction Model;
• What aspects of the represented world are being represented and what aspects of the representing worlds are doing the representing, which introduces the Instructional Model and the Context Model;
• The correspondence between the represented and the representing worlds, which focuses on a key element of the DeFT framework, the translation between MERs.

Figure 1

An overview of the four models of DEMIST.

Figure 1

An overview of the four models of DEMIST.

The DeFT framework does not apply to all aspects of an IS. The major of influence of DeFT is on the design of the ERs in the Interaction Model and how the MERs are used in the Context Model. It is also important to note that our environment was designed for experimental purposes and not as a full blown authoring instructional simulation environment. It is domain-specific and the design features are restricted accordingly. However, such a modular architecture will allow us to extend the software toward more domain-independence in the future.

3.1. The represented world

Ideally, the domain chosen for this investigation should support many features of multi-representational learning. It should require complex learning tasks to be undertaken so that more functions of MERs are likely to be needed and so that the associated cognitive tasks are not trivial. The domain should be described by a number of different representations rather than one predominant representation (flexibility in form) and should involve a number of dimensions of information so that distributed of information across representations can be considered (flexibility in redundancy). Finally, to explore how MERs may encourage deeper understanding it would be beneficial if the domain could be considered as both a concrete problem and as an instantiation of a more abstract idea (flexibility of function). These considerations led us to choose Prey-Predator relationships as a suitable model to explore learning with MERs.

The Simulation Model is defined by a set of mathematical models. This set can provide the learner with situations that progress from simple to complex and from less to more realistic (i.e. to instantiate model progression ). These models include, in increasing complexity, Single-Species with Unlimited Growth, Single-Species with Limited Growth, Two-Species with Simple Predation. Each model is composed of a formal definition plus an associated natural language description. For example, the mathematical model for Single-species with Limited Growth is the following equation: dN/dt = r * N * ( 1 – N/K)

3.2. The representing world

The Interaction Model defines the ERs used in a scenario. Many representations are available including tables, graphs, charts, phase-plots and population density diagrams (see Figure 2). Each plays a different role in supporting understanding of the predator-prey relationship. For example, the table allows quick and accurate read-off of values; the graph shows patterns and highlights such features as maxima and minima in populations and the phase-plot reveals quadrants of activities and stability of the environment.

Figure 2

Three examples of ERs displaying the dimensions of information of a Two-Species with Limited Predation model: a population density (left), a table (middle) and a histogram (right).

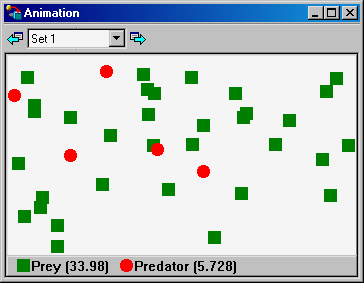
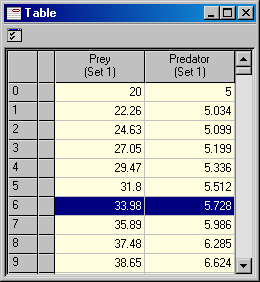
Figure 2

Three examples of ERs displaying the dimensions of information of a Two-Species with Limited Predation model: a population density (left), a table (middle) and a histogram (right).

The design of a particular external representation relies on three kinds of elements. Outcomes specifies what elements of the represented world are displayed in the ER. Format describes how the representation encodes and presents information to the learner. For a table, specifying format could include factors such as the precision of the displayed values. Actions specifies the interactions modes that apply to the ER. These actions can be classified in three categories: actions available only for authoring purpose (e.g. specifying the outcomes accessible during learning), actions that result in only local changes (e.g. choosing the outcomes to display) and actions that refer to translation between ERs.

3.3. What is represented and what is doing the representing

The Instructional Model of DEMIST describes the way a formal model is represented to the learner in a pedagogically useful way and defines the available instructional activities. Instructional activities are focused on representational interactions. The first elements of the instructional model are the aggregates (i.e. the pedagogically interesting aspects of the formal representations). For example, from the Single-species with Limited Growth model, an aggregate such as PreyIncreaseRate (r*(1–N/K)) can be defined. Activities occur at breakpoints where learners can develop hypotheses (e.g. “What will be the density of prey in 50 steps?”) or perform actions (e.g. “A harsh winter decreases prey density by 50%. Analyse its effects on predator density”) or translate information across representations (e.g. “What should the size of the prey icon be if the table is currently showing 6.2”).

The Context Model is the central part of the DEMIST authoring process. It organises the information from the simulation, interaction and instruction models into a useable form. It is where most of the key design parameters of DeFT (i.e. redundancy, form, translation, sequence and number) are instantiated. It includes a set of learning units, each defined in association to a single simulation model. They are related to instructional models, thus providing them with a dedicated set of activities and a set of available aggregates.

Figure 3

Snapshot of the Context Design interface.

Figure 3

Snapshot of the Context Design interface.

Each experimental set is defined by setting initial values and key parameters, allowing learners to run multiple experiments, (e.g. to compare Prey Density with different Carrying Capacities). This feature provides more opportunities to explore informational redundancy.

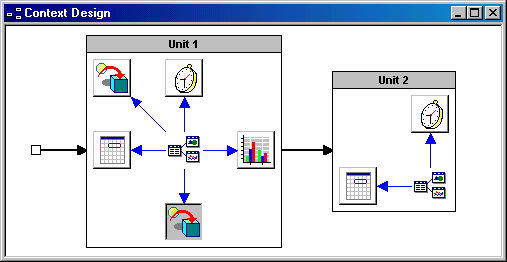
The final step consists of adding the interfaces to the ERs required by the simulation scenario and defined in the interaction model (see Figure 3). The nature of ERs available in each scenario is specified. For example, two representations with different formats can be included, allowing us to study how the form of the multi-representational system influences learning. We can also state a maximum number of co-present ERs: if learners want to activate another one, they have to close one of the opened one. This sequencing of representations can be specified during authoring, or left to a learner’s initiative.

3.4. The correspondence between represented world and representing worlds

There is a non-isomorphic relationship between domain concepts and their representation at the interface. To identify and respond to learners’ manipulation of these underlying concepts when they are only ever able to act on the ERs, it necessary to clearly separate domain specification from interface specification mechanisms. To achieve a clearly organised environment, we applied the 4-level knowledge organisation methodology proposed by and used to design a 3D dynamic geometry microworld, CALQUES 3D . It describes each concept in the domain in the following way (see Figure 4):

• The Domain level, is the most abstract and contains theoretical information independently of any symbolic-level representation (e.g. the description of the prey-predator relationships, the assumptions made for modelling, etc.);
• The Internal Unified Representation level, consists of a computational realisation of the domain concepts, in a unique and single form that is accessed by every component of the environment (e.g.. data structures and methods that implement the mathematical formulae, the dimensions of information and the aggregates, etc.);
• The External Presentation level is a reification of the represented concepts, which defines the nature of the ER. (e.g. their format and operators);
• The Interface level is a physical instantiation of the ER at the graphical interface.

This methodology provides many advantages for implementing learning environments . We use it to ensure the graphical coherence of concepts at the interface and to identify and interpret actions of the learners at a more cognitive level.

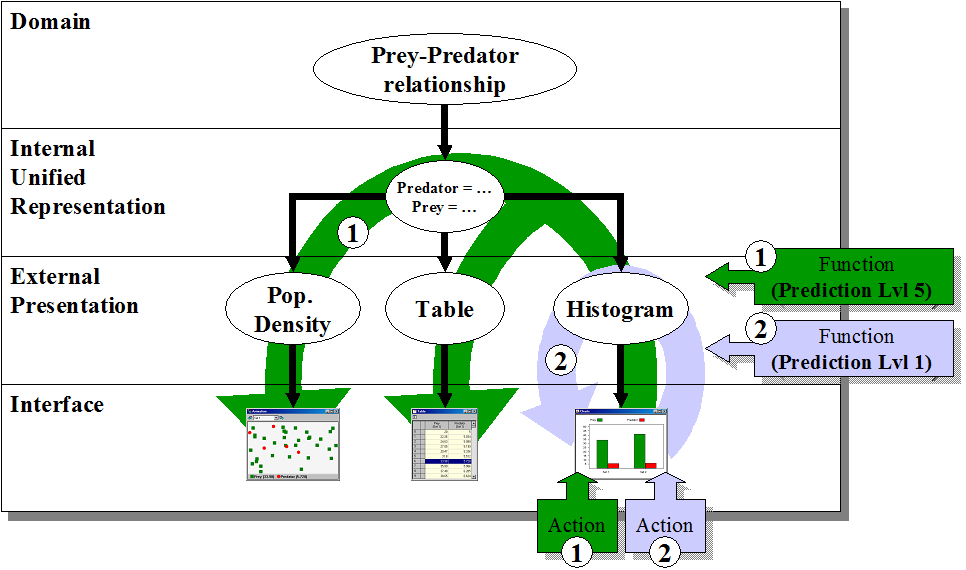
Figure 4

A knowledge representation model in 4 levels showing two alternative actions.

Figure 4

A knowledge representation model in 4 levels showing two alternative actions.

This can be seen by considering how its supports the multiple levels of translation provided by DEMIST. A translation action is defined both by the nature of the ER and by the level of translation specified in the context model. For example, a learner may be one required to predict the value for a population given particular configurations of parameters. Thus, a learner might be asked, in a histogram ER, to estimate the number of Prey in 50 steps time (see Figure 4). When the level of translation is set to full dyna-linking (level 5), the action (e.g. dragging the top of the appropriate bar to a new position, labelled ①) is interpreted within the Histogram ER and associated with the function Prediction (Level 5). As this is a global action, the function is applied to the unified representation and then this is echoed onto every ER, which results in appropriate feedback at the interface (e.g. the bar is modified in the Histogram, a value is added to the Table, individuals are added to the Population Density ER). When the level of translation is set to complete independence (level 1, see ②) the same action is interpreted and associated with the function Prediction (Level 1). As this is a local action, it does not modify the unified representation, so the only effects of this function are on the Histogram ER, where the relevant feedback is displayed (e.g. the bar is increased). No information is added to the other ERs - the learner must add this information by himself or herself in every other ER.

4. Conclusion

DEMIST is a multi-representational simulation environment that is designed to allow systematic exploration of the key parameters identified in DeFT. By designing the environment in the way we have described, we can quickly and easy author a range of multi-representational scenarios that differ in terms of informational redundancy, form, automatic translation, sequence of presented representation and number visible at any one time. For example, systems can be created which only include representations that have exactly the same information (full redundancy) to ones in which each representations conveys unique information (no redundancy). Authors can create systems that include representations of many different forms (multiple modalities, levels of abstraction, etc). There is no theoretical limit to the number of representations that can be presented at any given time, although we can set this limit in authoring mode. Representations can be co-present, can be switched between under learner control or learners can be given a predetermined sequence of representations. Finally and, uniquely amongst simulation environments to our knowledge, translation between representations can be varied from full dyna-linking through to complete independence.

We are now conducting a series of experiments exploring how these design parameters influence learning. The initial study is formative in nature exploring how learners adjust to an environment with so much representational flexibility and one which varies the level of translation between representations. It also is investigating if learners can be rational representation users – i.e. do they chose appropriate representations for the task and their level of understanding. Subsequently, we intend to explore predictions concerning how different design parameters impact upon learning and ultimately aim to uncover design principles for how best to support the different functions of MERs.

5. References